【密码学】椭圆曲线密码 ECC

source. 12月 20, 2020

RSA密钥长度太长，计算较慢。亲，来试试ECC吧！

椭圆曲线密码学（Elliptic Curve Cryptography，ECC）是一种基于椭圆曲线数学的非对称加密算法，安全性基于椭圆离散对数问题。

优势：ECC 使用较短的密钥就能达到与更长密钥的 RSA 相当等级的安全性。被广泛用于 HTTPS、SSH、PGP 协议以及比特币（BTC）、以太币（ETH）上。

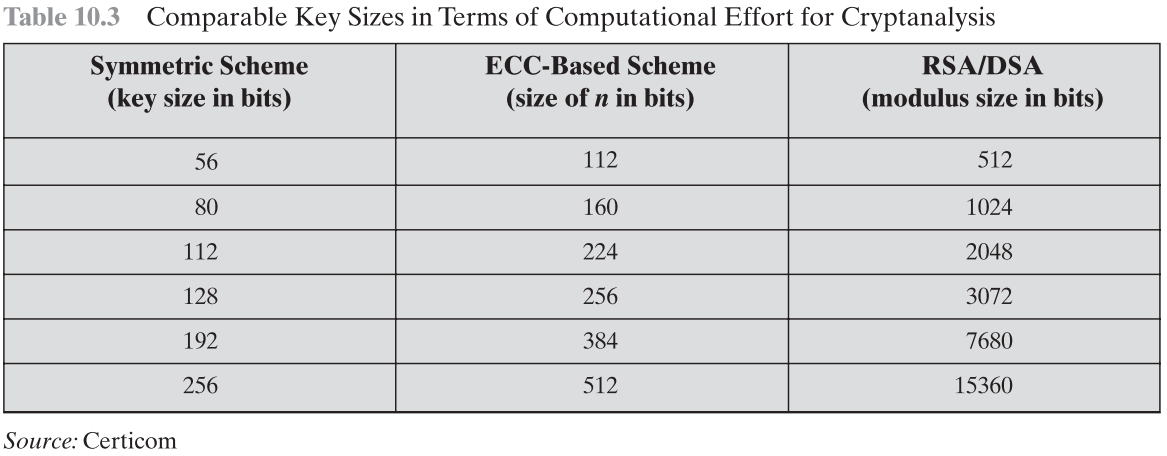
~~ECC 有取代 RSA 的趋势，ECC 是下一代非对称加密算法！~~

缺陷：可能被藏了后门，可信度还没有 RSA 高，而且可能涉及专利。

椭圆曲线

椭圆曲线 $E(a,b)$ 由如下形式的方程定义：

$y^2=x^3+ax+b$

并且要保证曲线不含奇点，即满足：

$4a^3+27b^2\ne 0$

椭圆曲线始终关于 $x$ 轴对称。

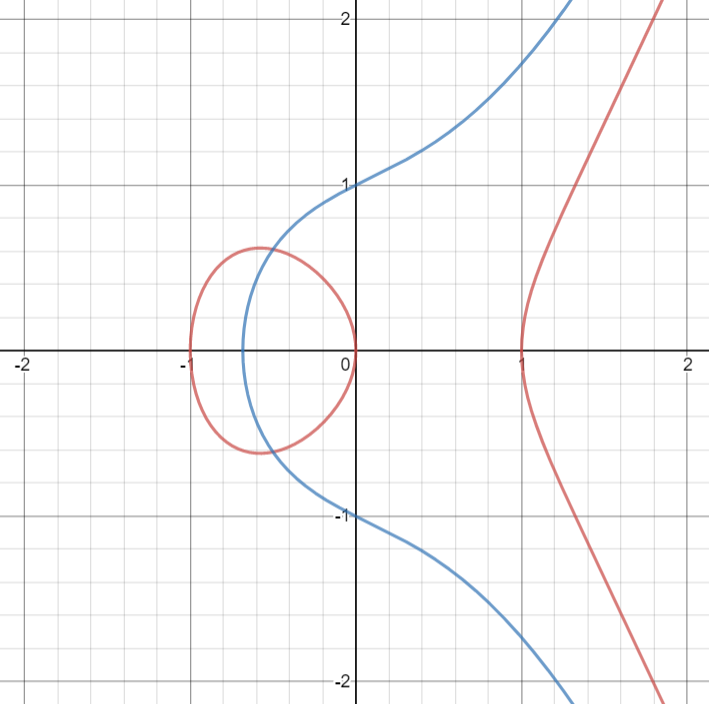
图中，红色为 $y^2=x^3-x$，蓝色为 $y^2=x^3+x+1$，作图工具：Desmos。

另外，椭圆曲线还需引入一个无穷处的点作为曲线的一部分，可以使用符号 $O$ 表示。

那么，椭圆曲线的表达式为：

$\left\{ (x, y) \in \mathbb{R}^2\ |\ y^2 = x^3 + ax + b,\ 4 a^3 + 27 b^2 \ne 0 \right\}\ \cup\ \left\{ O \right\}$

群

一个群（group）$G$ 由一堆元素和一个运算（加法 $+$）组成，必须满足四个条件：

封闭性：若 $a\in G$ 且 $b\in G$，则 $a+b\in G$
结合律：若 $a,b,c\in G$，则 $(a+b)+c=a+(b+c)$
单位元：对于每个 $a\in G$，$a+O=O+a=a$
逆元：对于每个 $a\in G$，都存在唯一的 $b\in G$，使得 $a+b=O$，称 $b$ 为 $a$ 的逆元

若一个群满足交换律，即 $a+b=b+a$，则称它为交换群或阿贝尔群。

若满足群的条件，则可以直接使用群的性质。比如，只有一个单位元，每个元素有且只有一个逆元。

椭圆曲线上的群论

可以在椭圆曲线上定义一个阿贝尔群：

群中的元素是椭圆曲线上的点
单位元是无穷处的点 $O$
$(x,y)$ 的逆元是 $(x,-y)$
加法规则：一条直线与 $E$ 交于三个点 $P,Q,R$，它们之和等于 $O$，即 $P+Q+R=O$
$+$ 运算满足交换律、结合律

加法的几何描述

由 $P+Q+R=0$ 有：

$P+Q=-R$

也就是做穿过 $P$ 和 $Q$ 两点的直线，它穿过的第三个点 $R=(x,y)$ 的关于 $x$ 轴对称的点 $(x,-y)$ 就是 $P+Q$ 的结果。

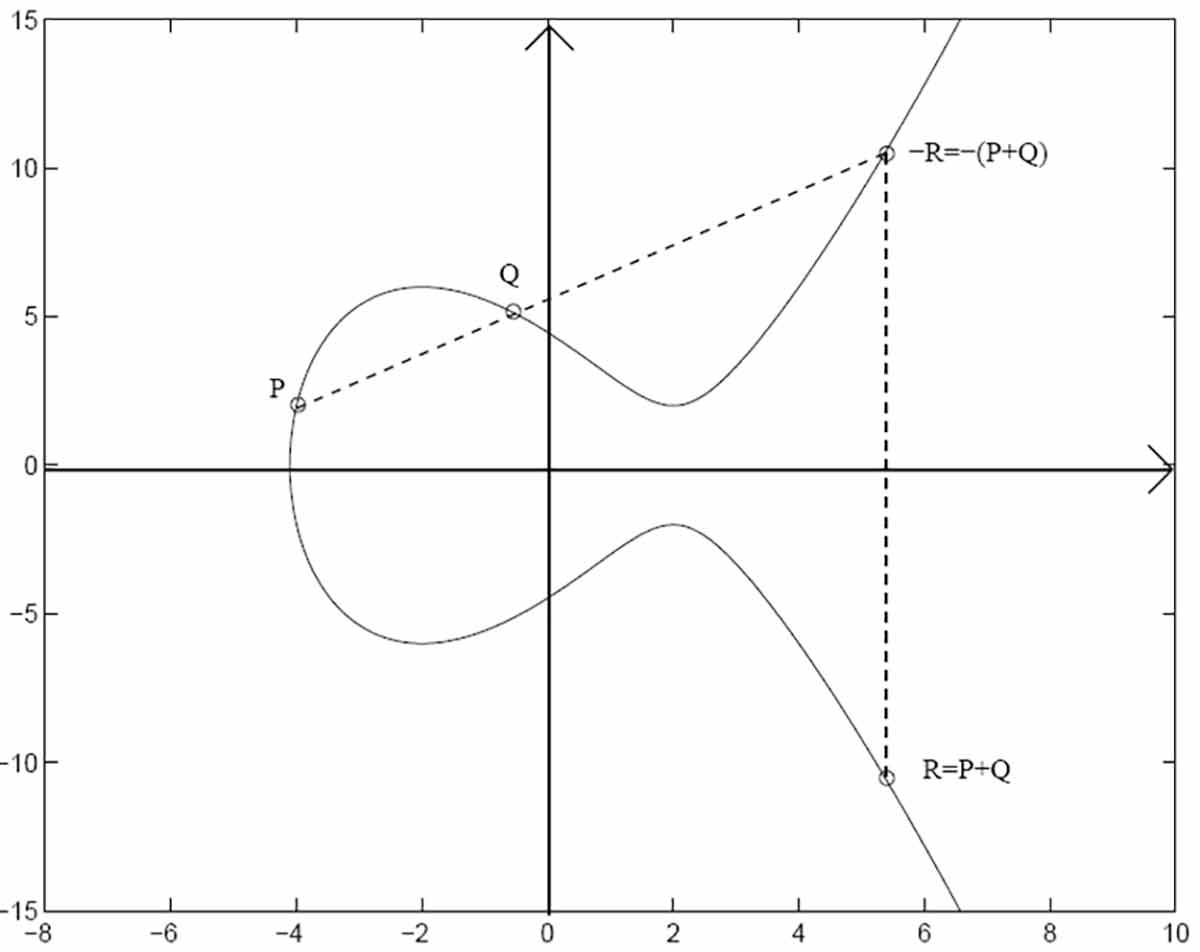
若 $P=Q$，那么这条直线是过点 $P$ 的切线。

实数域上加法的代数描述

一元三次方程的解，直接用公式吧少年。（老师都不想细讲）

椭圆曲线公式：

$y^2=x^3+ax+b$

当$P\ne Q$时：

$\begin{align} \Delta &= \frac{y_Q-y_P}{x_Q-x_P}\\ x_R&=\Delta ^2-x_P-x_Q\\ y_R&=-y_P+\Delta (x_P-x_R) \end{align}$

当$P=Q$时：

$\begin{align} x_{R}&=\left(\frac{3 x_{P}^{2}+a}{2 y_{P}}\right)^{2}-2 x_{P}\\ y_{R}&=\left(\frac{3 x_{P}^{2}+a}{2 y_{P}}\right)\left(x_{P}-x_{R}\right)-y_{P} \end{align}$

$\mathbb{Z}_p$上加法的代数描述

设变元$x,y$和椭圆曲线参数$a,b$都在$\mathbb{Z}_p$上取值，椭圆曲线公式两边取模$p$得到$E_p(a,b)$：

$y^2\bmod p=(x^3+ax+b)\bmod p$

求$P+Q$：

$\begin{align} x_R&=(\lambda^2-x_P-x_Q)\bmod p\\ y_R&=\left(\lambda(x_P-x_R)-y_P \right)\bmod p \end{align}$

其中，

$\lambda=\left\{\begin{array}{ll} \left(\frac{y_{Q}-y_{P}}{x_{Q}-x_{P}}\right) \bmod p & \text { if } P \neq Q \\ \left(\frac{3 x_{P}^{2}+a}{2 y_{P}}\right) \bmod p & \text { if } P=Q \end{array}\right.$

$\operatorname{GF}(2^m)$上加法的代数描述

设变元$x,y$和椭圆曲线参数$a,b$都在$\operatorname{GF}(2^m)$上取值，得到$E_{2^m}(a,b)$：

$y^2+xy=x^3+ax^2+b$

~~大型懵逼现场！~~反正考试也不太可能会考。

若$P=(x_P,y_P)$，则$-P=(x_P,x_P+y_P)$。

若$P\ne Q,~P\ne-Q,~R=P+Q$，则：

$\begin{align} \lambda&=\frac{y_{Q}+y_{P}}{x_{Q}+x_{P}}\\ x_{R}&=\lambda^{2}+\lambda+x_{P}+x_{Q}+a \\ y_{R}&=\lambda\left(x_{P}+x_{R}\right)+x_{R}+y_{P} \end{align}$

若$R=P+P$，则：

$\begin{align} \lambda&=x_P+\frac{y_P}{x_P}\\ x_R&=\lambda^2+\lambda+a\\ y_R&=x_P^2+(\lambda+1)x_R \end{align}$

伽罗瓦域可以极大扩展可能取值？

ECC

ECC的安全性基于椭圆曲线上的离散对数问题，考虑方程$Q=kP$：

已知$k,P$，计算$Q$容易
已知$P,Q$，计算$k$困难

ECC Diffie-Hellman

和ElGamal一样，它的安全性也基于离散对数问题，很快想到，可以往DH上套：

选定一个大的模数$q$（两种形式：素数$p$或$2^m$，分别对应上面两种域）以及系数$a$和$b$，由此定义椭圆曲线$E_q(a,b)$，并在其上挑选一个基点$G=(x_g,y_g)$，它的阶$n$（使得$nG=O$成立的最小正整数）是一个非常大的数。$E_q(a,b)$和$G$均公开。
Alice选择一个小于$n$的整数$n_A$作为私钥，计算公钥$P_A=n_AG$并公开
Bob选择一个小于$n$的整数$n_B$作为私钥，计算公钥$P_B=n_BG$并公开
Alice计算密钥$K=n_AP_B=(n_An_B)G$，Bob计算密钥$K=n_BP_A=(n_An_B)G$。

这样，Alice和Bob就通过不安全信道建立起了密钥$K$。

注意：上述过程中的加法、数乘运算均是椭圆曲线下的运算。

ECC 加解密

和ElGamal一样，本质上就是通过DH协商一个密钥，然后用这个密钥进行加解密。

密钥生成：

协商椭圆曲线$E_q(a,b)$和基点$G=(x_g,y_g)$
Alice选择一个私钥$n_A$，计算公钥$P_A=n_AG$并公开
Bob选择一个私钥$n_B$，计算公钥$P_B=n_BG$并公开

假设Bob要给Alice发一个消息$M$：

Bob使用自己的私钥$n_B$和Alice的公钥$P_A$计算共同密钥$K=n_BP_A=(n_An_B)G$
Bob发送$c_1=P_B,~c_2=K+M$

Alice收到密文，解密过程：

Alice计算共同密钥$K=n_Ac_1=n_AP_B=(n_An_B)G$
Alice解密消息$M=c_2-K$

若$K=(x_K,y_K)$，则$-K=(x_k,-y_K)$。

再次提醒：上述过程中的加法、数乘运算均是椭圆曲线下的运算。

Online Calculator

ECCalculator - christelbach - $\mathbb{Z}_p$下的加法

Python Code

def ecAdd(P, Q, a, b, p):
    x_P, y_P = P
    x_Q, y_Q = Q
    if P == Q:
        lmd = (3*x_P*x_P+a)*pow(2*y_P,-1,p)%p
    elif x_P == x_Q:
        return (0, 0)
    else:
        lmd = (y_Q-y_P)*pow(x_Q-x_P,-1,p)%p
    x_R = (lmd*lmd-x_P-x_Q)%p
    y_R = (lmd*(x_P-x_R)-y_P)%p
    return (x_R, y_R)


def ecTimes(n, P, a, b, p):
    R = P
    for i in range(2, n+1):
        R = ecAdd(P, R, a, b, p)
        # print('{}P = ({}, {})'.format(i, R[0], R[1]))
    return R

椭圆曲线数乘运算 ecTimes() 可用类似快速幂的形式优化，但本人懒，就酱。

参看

密码编码学与网络安全——原理与实践（第七版）

椭圆曲线密码学 - Wikipedia

ECC椭圆曲线加密算法介绍 - 知乎

总结

终于知道本科的时候为什么不学且不考ECC了：

看着很玄学
推导略复杂
做题套公式，计算复杂且易出错

~~说实话我觉得把公式贴在这里都是浪费时间。~~

读书患不多，思义患不明，患足己不学。既学患不行。

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自 ComyDream 。
本文链接：http://comydream.github.io/2020/12/20/cryptography-ecc/