【密码学】公钥密码之 ElGamal
神奇的离散对数问题,老师提出了密钥交换,学生在此基础上提出公钥加密算法。
Diffie-Hellman 密钥交换协议
迪菲-赫尔曼密钥交换 (Diffie-Hellman key-exchange, DH) 基于离散对数问题这一数学困难问题,可以让通信双方在完全没有对方任何预先信息的条件下,通过不安全信道创建一个密钥。于1976年首次发表。
这里的离散对数问题,指的是:
- 已知 $a,b,n$ ,计算 $a^b\bmod n$ 是简单的。
- 已知 $a,(a^b\bmod n),n$ ,计算 $b$ 是困难的。
Diffie-Hellman 密钥交换过程:
- Alice 和 Bob选定一个素数 $p$ ,以及它的一个原根 $g$ 。
- Alice 选择一个密钥 $a$ ,计算 $A=g^a\bmod p$ ,发给 Bob 。
- Bob 选择一个密钥 $b$ ,计算 $B=g^b\bmod p$ ,发给 Alice 。
- Alice 计算 $s=B^a\bmod p$ ,Bob 计算 $s=A^b\bmod p$ 。
这样,Alice 和 Bob 就共享了一个密钥 $s=g^{ab}\bmod p$ 。
通俗理解:在调色板上将两种颜色混合容易,而将两种颜色分开是困难的。
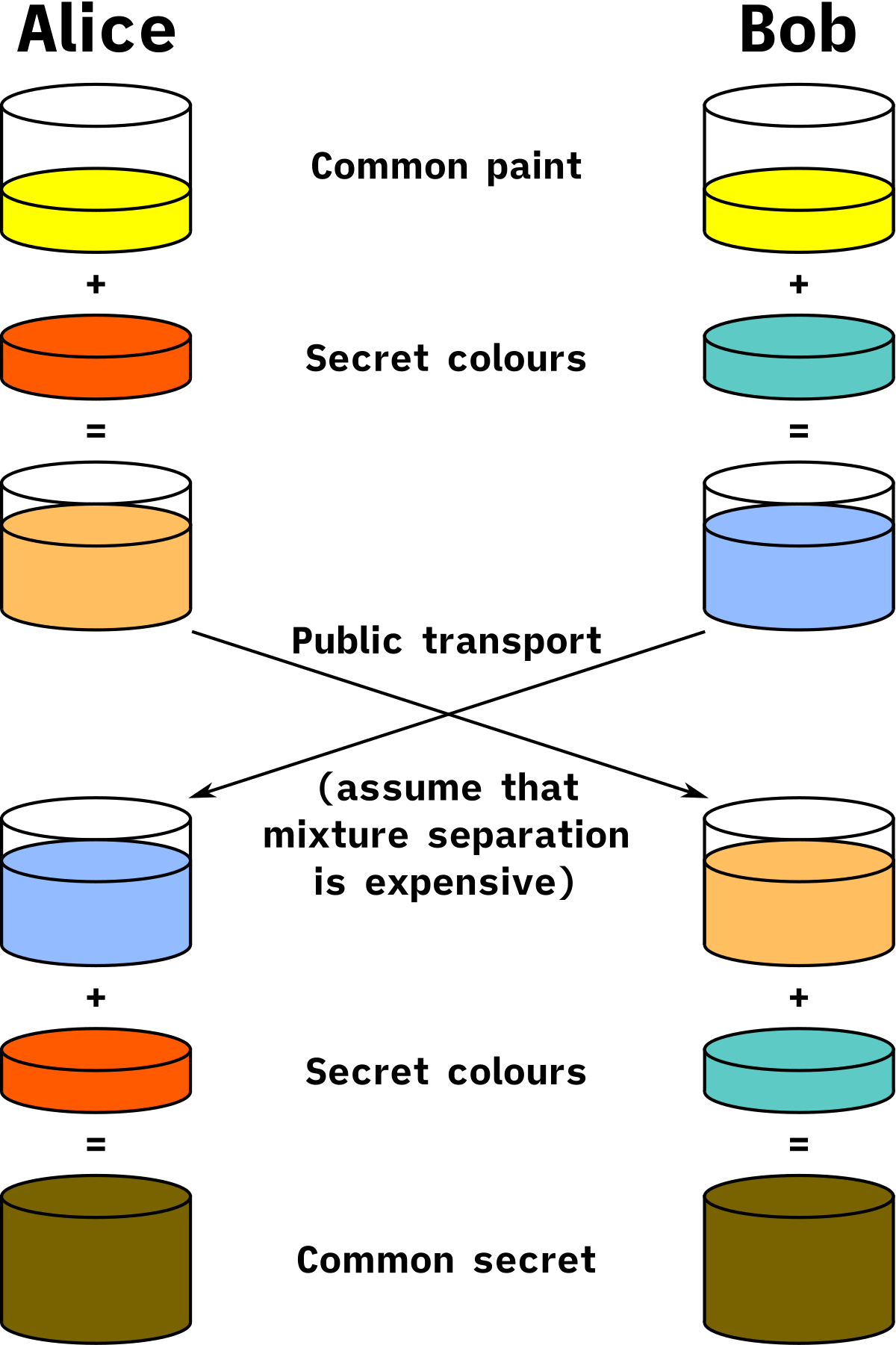
由于离散对数问题是一个数学困难问题,在选择了合适的 $p$ 和 $g$ 时,Diffie-Hellman 密钥交换协议被认为是「窃听安全」的。攻击者 Eve 在已知 $p,~g,~(g^a\bmod p),~(g^b\bmod p)$ 的情况下,难以计算出 $s=g^{ab}\bmod p$ 。
缺陷:无法抵抗中间人攻击
最初,DH 本身没有提供任何身份认证,因此容易遭受中间人攻击。
- 中间人 Eve 假装自己是 Bob 与 Alice 通信 $s_1=g^{ac}\bmod p$ 。
- 中间人 Eve 假装自己是 Alice 与 Bob 通信 $s_2=g^{bc}\bmod p$ 。
- Eve 将 Alice 发来的消息用 $s_1$ 解密,使用 $s_2$ 加密,发送给 Bob 。
- Eve 将 Bob 发来的消息用 $s_2$ 解密,使用 $s_1$ 加密,发送给 Alice 。
- Alice 和 Bob 对此一无所知,还无知地以为在与对方通信。
因此,亟需一种能验证通信双方身份的机制 (如签名) 来防止这类攻击。
ElGamal 加密算法
ElGamal 加密算法 - 维基百科
T. ElGamal. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. CRYPTO ’84
T. ElGamal. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. TIT ’85
ElGamal 加密算法是一个基于 DH 的非对称加密算法 (基于离散对数难题) ,于 1985 年被提出。
本质上就是用 DH 获得一个密钥,然后用它加解密消息。
密钥生成:
- Alice 和 Bob 选定一个素数 $p$ ,以及它的一个原根 $g$
- Alice 选择一个私钥 $X_A$ ,计算公钥 $Y_A=g^{X_A}\bmod p$ ,公开
- Bob 选择一个私钥 $X_B$ ,计算公钥 $Y_B=g^{X_B}\bmod p$ ,公开
假如 Bob 要给 Alice 发送一条消息 $m$ ,加密过程:
- Bob 计算密钥 $k=(Y_A)^{X_B}\bmod p=g^{X_A X_B}\bmod p$
- Bob 发送 $c_1=Y_B,~c_2=km\bmod p$
Alice 收到密文,解密过程:
- Alice 计算密钥 $k=(c_1)^{X_A}\bmod p=(Y_B)^{X_A}\bmod p=g^{X_A Y_A}\bmod p$
- Alice 解密消息 $m=(c_2\cdot k^{-1})\bmod p$
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2020/12/19/cryptography-dh-elgamal/