【密码学】公钥密码之 RSA
你有没有想过一个问题,在对称密码体制中,密钥一般经过「安全信道」传输,那么怎么建立安全信道呢?
公钥密码体制
问题的提出:对称密码的缺陷
如何建立「安全信道」
密文可以在公开信道上直接传输,但是密钥需要在「安全信道」上传输,那么问题来了,如何建立「安全信道」?
有人可能会说,可以提前商量好。
想象一下,在互联网上,你和对方有很大概率是「陌生人」,你们第一次「见面」,如何提前商量好?
密钥分发和管理的困难
对于一个有 $n$ 个通信方的实体,两两要进行安全通信的话,每个实体要拥有 $n-1$ 个密钥,所有通信方需要 $C_n^2=n(n-1)/2$ 个密钥。
因为对称密码有这些缺陷,有人提出了「公钥密码」。
是啥
Asymmetric actually means that it works on two different keys i.e. Public Key and Private Key. As the name describes that the Public Key is given to everyone and Private key is kept private.
有两个密钥:加密密钥(公钥)与解密密钥(私钥) ,两者并不相同。加密密钥是公开的。且由加密密钥得到解密密钥在计算上不可行。
类比
任何人只需按一下(听到咔哒一声)就可以把锁合上,但只有持有钥匙的人才能把锁打开。关锁(加密)是容易的,人人都可以做到,但开锁(解密)只能由有钥匙的人来做。知道关锁的知识无助于开锁。
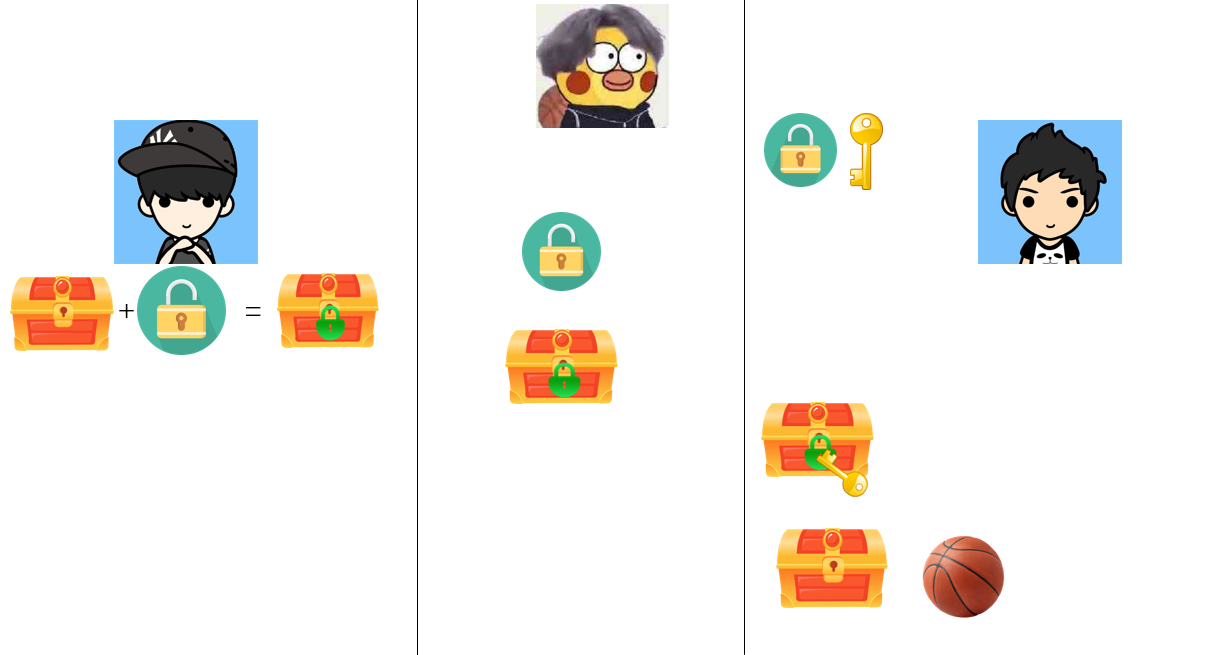
步骤
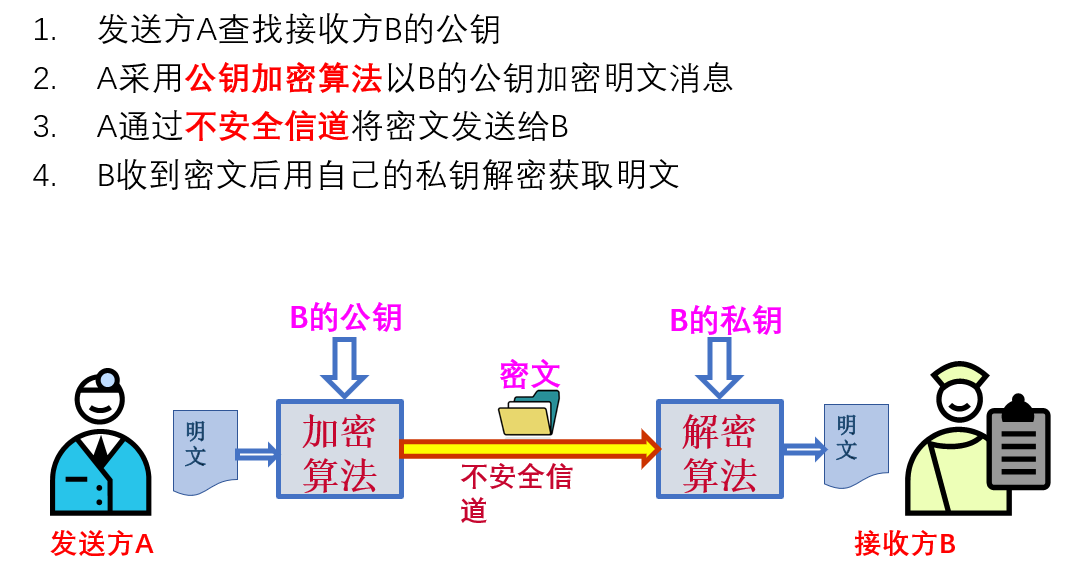
实际使用
现在一般使用对称密码和公钥密码相结合的方式实现数据加密。
公钥密码体制建立在数学困难问题上,加解密效率较低。一般用于(建立「安全信道」)传输对称密码的密钥。而消息一般是以对称密码体制加密的。
RSA
它的安全性基于大整数的因数分解的困难性。
任意生成两个大素数 $p$ 和 $q,$由他们计算 $n = p\cdot q$ 是容易的,但由 $n$ 分解出 $p$ 和 $q$ 是困难的。
其中,公钥为$(n,e)$,私钥为$d$(有些地方也写成$(n,d)$ )。
如何生成大素数?
在这里,我们先回顾《信息安全数学基础》中学的费马小定理和 Miler-Rabin 算法。
费马小定理
若 $a$ 是一个整数, $p$ 是一个素数,那么 $a^p-a$ 是 $p$ 的倍数。
若又满足 $\gcd(a,p)=1$,则 $a^{p-1}-1$ 是 $p$ 的倍数。
Miler-Rabin 算法
大整数的素性测试一般采用 Miller-Rabin 算法。它是一个基于概率的算法,是费马小定理的一个变换。
要测试 $n$ 是否为素数,首先将 $n-1$ 分解为 $2^s d$ 。其中,$s$和$d$都是正整数,且$d$是奇数。
在每次测试开始时,先随机选一个介于 $[1, n-1]$ 的整数 $a$ ,之后如果对所有的 $r \in [0, s-1]$ ,若$ a^d \bmod n \neq 1$ 且 $a^{2^{r}d} \bmod n \neq -1$,则 $n$ 是合数。否则,$n$ 有 $0.75$ 的概率为素数。增加测试的次数,该数是素数的概率会越来越高。
这样,我们就可以给定位数 $n$ 的情况下随机生成数,然后再用 Miller-Rabin 算法验证它是不是素数,若不是,则再随机生成其他数字,循环。Python 脚本如下:
import random
# 素性检验:采用 Miler-Rabin 检验法
def miller_rabin(n, k=80):
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
r, s = 0, n - 1
while s % 2 == 0:
r += 1
s //= 2
for _ in range(k):
a = random.randrange(2, n - 1)
x = pow(a, s, n)
if x == 1 or x == n - 1:
continue
for _ in range(r - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
# 生成 b 位的素数
def genPrime(b=1024):
while True:
# the highest bit must be 1
ans = "1"
for i in range(b-2):
ans += str(random.randint(0,1))
# the lowest bit must be 1
ans += "1"
ans = int(ans,2)
if miller_rabin(ans):
return ans
我们可以肯定的是:最高位一定是1(否则它就不是 n 位了,而是小于 n 位)。最低位也一定是 1(因为它是素数,刨除 2 的情况,则一定是奇数)。
如何快速求带模的幂运算?
加密和解密过程都用到了幂运算,那么怎么快速求呢?
原理:模重复平方运算,Python 代码如下:
# Fast mod: Calculate pow(x,n) mod m
# x: Base number
# n: Exponent
# m: Modulus
def FastMod(x, n, m):
a = 1
b = x
while True:
temp = n
if n % 2 == 1 :
a = a * b % m
b = b * b % m
n = n//2
if temp < 1 :
return a
但是,经测试,自己写的模重复平方运算并没有 Python 的内置函数 pow(x,n,m) 快(说明内置函数有进行优化),故直接采用 Python 内置函数:
pow(x,n,m)
完整代码
RSA_tables.py
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import random
# Fast mod: Calculate pow(x,n) mod m
# x: Base number
# n: Exponent
# m: Modulus
def FastMod(x, n, m):
a = 1
b = x
while True:
temp = n
if n % 2 == 1 :
a = a * b % m
b = b * b % m
n = n//2
if temp < 1 :
return a
# computeD: Known phi(n) and e, calculate d
# d ≡ e'(mod phi(n))
# e: the public (or encryption) exponent
# phi_n: Euler totient function phi(n) = (p-1)*(q-1)
def computeD(e, phi_n):
(x, y, r) = extendedGCD(phi_n, e)
# y maybe < 0, so convert it
if y < 0:
return phi_n + y
return y
# Extended Euclidean algorithm
def extendedGCD(a, b):
# a*xi + b*yi = ri
if b == 0:
return (1, 0, a)
# a*x1 + b*y1 = a
x1 = 1
y1 = 0
# a*x2 + b*y2 = b
x2 = 0
y2 = 1
while b != 0:
q = a / b
# ri = r(i-2) % r(i-1)
r = a % b
a = b
b = r
# xi = x(i-2) - q*x(i-1)
x = x1 - q*x2
x1 = x2
x2 = x
# yi = y(i-2) - q*y(i-1)
y = y1 - q*y2
y1 = y2
y2 = y
return(x1, y1, a)
def str2Hex(m):
return "".join("{:02x}".format(ord(x)) for x in m)
# 素性检验:采用 Miler-Rabin 检验法
def miller_rabin(n,k=80):
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
r, s = 0, n - 1
while s % 2 == 0:
r += 1
s //= 2
for _ in xrange(k):
a = random.randrange(2, n - 1)
x = pow(a, s, n)
if x == 1 or x == n - 1:
continue
for _ in xrange(r - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
# 生成 b 位的素数
def genPrime(b=1024):
while True:
# the highest bit is 1
ans = "1"
for i in range(b-2):
ans += str(random.randint(0,1))
# the lowest bit is 1
ans += "1"
ans = int(ans,2)
if miller_rabin(ans):
return ans
# Generate the encryption index: e
# 通常来说,e不需要太大,这样可以大幅提高加密效率。
# 我们可以生成一个素数,若它不是φ(n)的因数,则(e,φ(n))=1
def genE(phi_n):
while True:
e = genPrime(b=random.randint(3,13))
if e == 3 or e == 5:
continue
if phi_n%e != 0:
return e
RSA.py
#!/usr/bin/python
# -*- coding: UTF-8 -*-
from RSA_tables import *
# RSA Encryption
# Public key: (n,e)
# c ≡ m^e (mod n)
def RSAEncrypt(m,n,e):
m = int(str2Hex(m),16)
print "m = "+str(m)
c = pow(m,e,n)
return c
# RSA Decryption
# Private key: d
# m ≡ c^d (mod n)
def RSADecrypt(c,d,n):
m = pow(c,d,n)
m = '{:x}'.format(m).decode('hex')
return m
def main():
# 生成两个大素数p和q
print "Generate p and q ......"
p = genPrime()
q = genPrime()
print "p = "+str(p)
print "q = "+str(q)
# 计算n = p*q
n = p*q
print "n = "+str(n)
# 计算φ(n) = p*q
phi_n = (p-1)*(q-1)
print "\nGenerate e ......"
# 生成一个和φ(n)互素的数e
e = genE(phi_n)
print "e = "+str(e)
m = "Hello CUMTer~"
# 加密算法
print "\n"+8*"*"+" Encryption "+8*"*"
Ciphertext = RSAEncrypt(m,n,e)
print "The Ciphertext is:(Decimal)\n\t"+str(Ciphertext)
# 解密算法
print "\n"+8*"*"+" Decryption "+8*"*"
# 使用私钥d,d是e模φ(n)的逆
d = computeD(e,phi_n)
print "d = "+str(d)
Plaintext = RSADecrypt(Ciphertext,d,n)
print "The Plaintext is:\n\t"+str(Plaintext)
if __name__ == '__main__':
main()
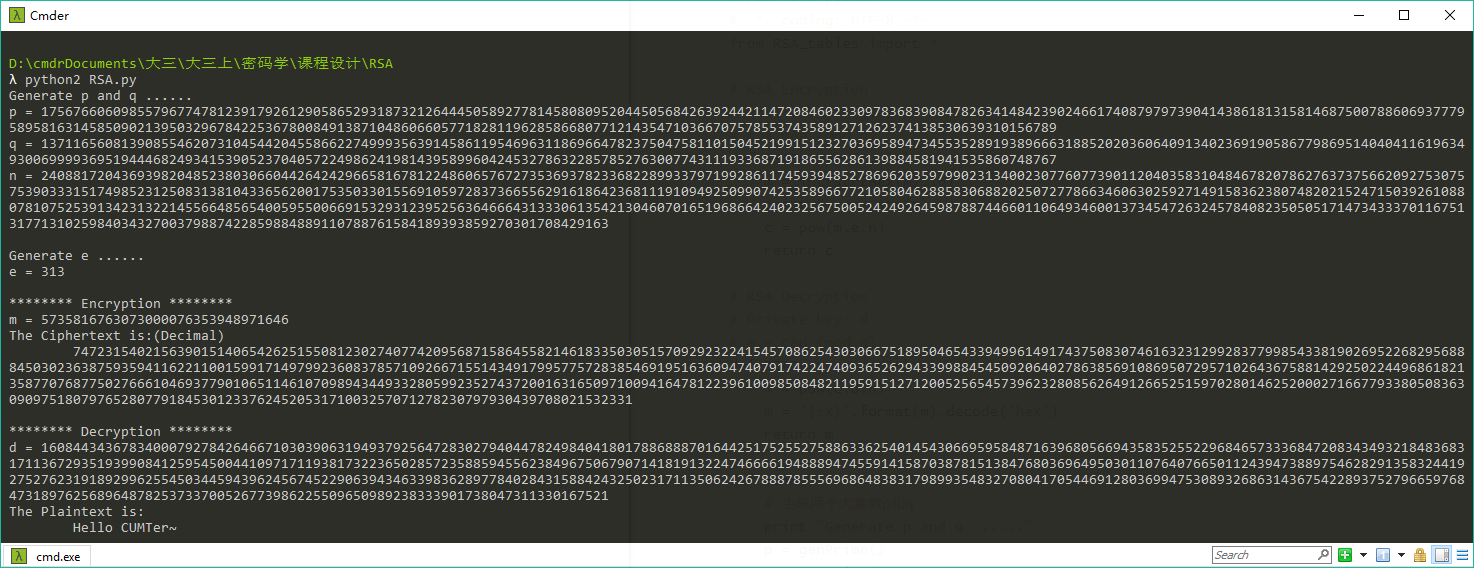
运行结果
安全性
非对称加密算法中 1024 bit 密钥的强度相当于对称加密算法 80bit 密钥的强度。但是,从效率上,密钥长度增长一倍,公钥操作所需时间增加约 4 倍,私钥操作所需时间增加约 8 倍,公私钥生成时间约增长16倍。所以,我们要权衡一下效率和安全性。一般来说, 1024 bit 只能用于加密 最多117 字节的明文。
低加密指数攻击
为了使加密高效,一般希望选取较小的加密指数 $e$ ,但是 $e$ 不能太小,否则容易遭到低加密指数攻击。
假设用户使用的密钥 $e=3$ 。考虑到加密关系满足:
则容易得到:
攻击者可以从小到大枚举 $k$ ,依次开三次根,直到开出整数为止。
攻击中,我们可以使用 Python 的 gmpy2 库中的 iroot(x, n) 函数,该函数接收两个参数,计算 x 开 n 次方的结果,它返回一个二元组 (y, b) ,如果开 n 次方的结果是整数,那么元组的第二项为 True ,利用这个我们可以很容易写出攻击脚本:
n = * # n=p*q
c = * # 密文
e = 3 # 一个低加密指数
i = 0
while 1:
if(gmpy2.iroot(c+i*n, e)[1] == True):
x = gmpy2.iroot(c+i*n, e)[0]
print '{:x}'.format(x).decode('hex')
break
i += 1
为防止低加密指数攻击,$e$ 通常不能取 3 。实际上,因为 $e$ 要和 $φ(n)$ 互素,所以能取到3的概率是很低的,但是并不说取不到,所以我们要完全避免这种情况。
这里我用我写的 RSA 算法举个例子,假设使用 $e=3$ 。
Generate p and q ......
p = 171455268636085257488077712615516009667578203105826538553947551155647673590611580614138833611608804000943824221603004994052565362477073809679492140069549862243645418245238197378515611203089963822440907111517561311547989163335825630216972556912580038590306843305030193924978560617579750807515959892708420715183
q = 171359550611582798079990266333298603333952864380038943444804495157928070877072224352343493181033443224708438060621636793006894532332588709185329713236648338355772948858632331943064199598364032825019035438811965490470700958037574316869226019908196902248769248095733274024159064108003854972864622650782289205507
n = 29380497783467776422804545342380884073073767724843562101514866933700515865199393798543164954322256286127996183107666598272991919505012006941533705239722905576667604963908296130704277310409724812040504843777293812384302836002890633501707787759661259399062131314822895394876387858791178490491341176880885426638430047466121225416225227277877402043531190227496988592230196087854904805556784742051662758925750021419949030387729236393798059814579004049870663701963107901659218176118607568953635817915399183454311233343208075308062083719884383257798034490003254766452927482694645243549811593935222784641768098639209802112781
Generate e ......
e = 3
******** Encryption ********
m = 5735816763073000076353948971646
The Ciphertext is:(Decimal)
188706042416761345172334239793248690073601891783556334684276552054586283936564932551473094136
把 $n, c, e$ 拿到攻击脚本去跑,很快(0.1s)就解出明文了。
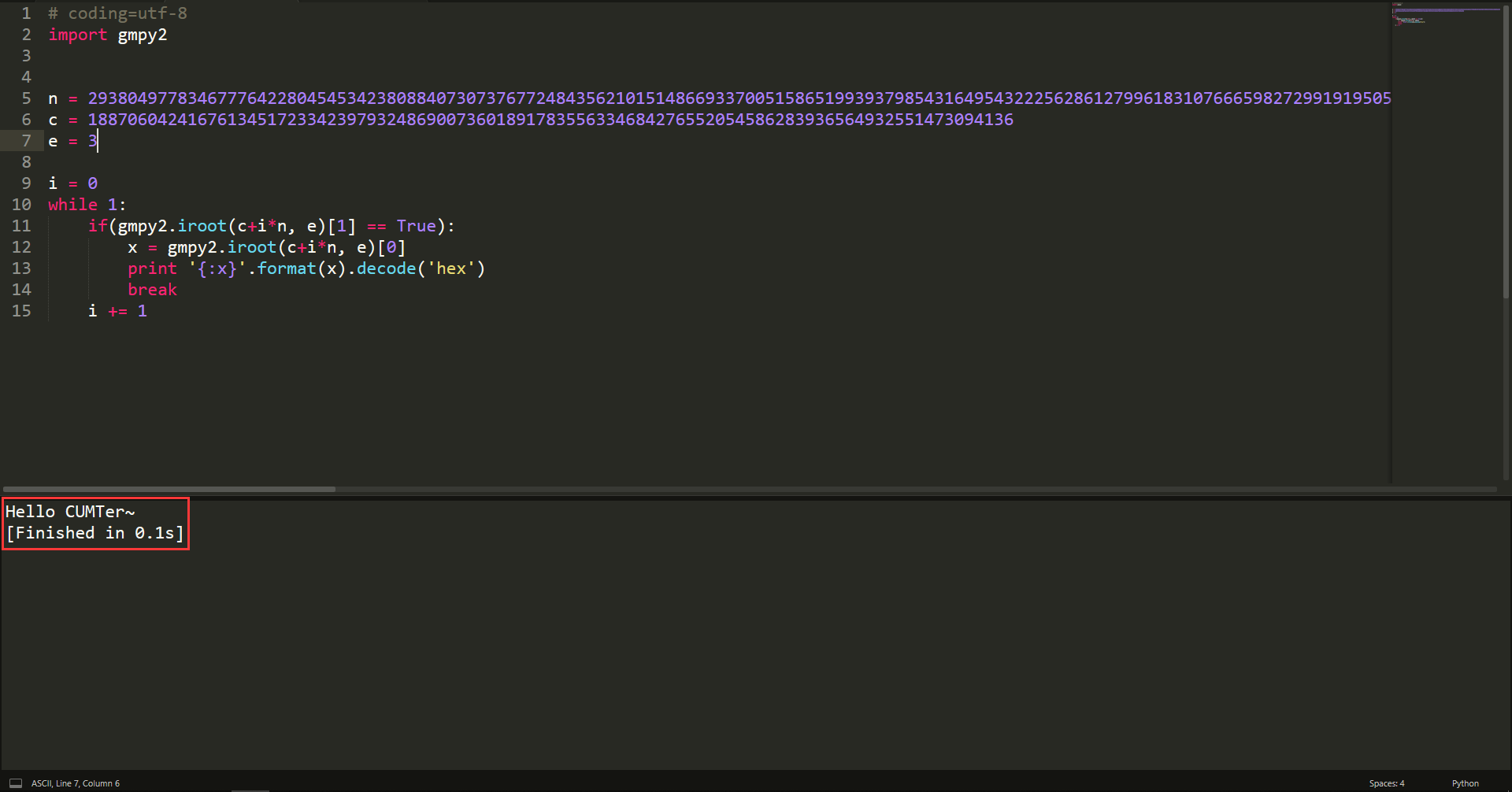
同样,其他低加密指数也难以抵挡这种攻击,我们应该尽量避免使用。
低加密指数广播攻击
还有一种情况是如果给 $k$ 个用户发的都是同个低加密指数比如 $e=3$ ,在不同的模数 $n_1.n_2,n_3$下 ,可由 CRT(中国剩余定理) 解出 $m^3$ ,从而直接开三次根解出 $m$。
共模攻击
场景:$n$ 相同(让多个用户使用相同的模数 $n$ ),但他们的公私钥对不同。这样,我们可以在已知 $n, e_1, e_2, c_1, c_2$ 的情况下解出 $m$ 。过程如下:
其实有个隐形的前提条件是:
也就是说,它们两个要互素。但其实,这个条件一般成立(因为我们选取的加密指数都是素数,两个不同素数彼此肯定互素)。
这样,由数论知识可以得出,存在 $s_1,s_2$ 使得:
成立,又由 RSA 定义可知:
易得出:
解出明文。
这样,我们仅需要使用扩展欧几里得算法求出 $s_1,s_2$ 便可解出明文,Python 脚本如下:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
# Extended Euclidean algorithm
def extendedGCD(a, b):
# a*xi + b*yi = ri
if b == 0:
return (1, 0, a)
# a*x1 + b*y1 = a
x1 = 1
y1 = 0
# a*x2 + b*y2 = b
x2 = 0
y2 = 1
while b != 0:
q = a / b
# ri = r(i-2) % r(i-1)
r = a % b
a = b
b = r
# xi = x(i-2) - q*x(i-1)
x = x1 - q*x2
x1 = x2
x2 = x
# yi = y(i-2) - q*y(i-1)
y = y1 - q*y2
y1 = y2
y2 = y
return(x1, y1, a)
n = *
c1 = *
c2 = *
e1 = *
e2 = *
s1,s2,r = extendedGCD(e1,e2)
if s1 < 0:
s1 = -s1
if s2 < 0:
s2 = -s2
m = pow(c1,s1,n)*pow(c2,s2,n)%n
ans = '{:x}'.format(m).decode('hex')
print ans
忘掉你所学的一切公式和定理,如果你还能利用自己的理解去推理出来,那就说明你的学问已经到家了。
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2018/12/30/cryptography-rsa/