【密码学】分组密码之 DES

Author Avatar
source. 12月 29, 2018
  • 在其它设备中阅读本文章

数据加密标准（Data Encryption Standard，DES）开创了公开密码算法的先例，极大地促进了密码学的发展。

分组密码

分组密码（Block Cipher）是将明文消息编码表示后的二进制序列，划分为固定大小的块，每块分别在密钥的控制下变换成等长的二进制序列。假设：

分别代表明文空间、密文空间、密钥空间、加密算法、解密算法，则有：

要求

  1. 分组应足够长，防止明文穷举攻击。
  2. 密钥应足够长，防止密钥穷举攻击。
  3. 由密钥确定的置换算法要足够复杂，足以抗击各种已知的攻击。
  4. 加密、解密算法要足够简单，易于软件和硬件的快速实现。

设计原则

1949 年，克劳德·香农（Claude Shannon）提出了密码学的两大原则：混淆（Confusion）和扩散（Diffusion），并引进了 SP 网络（Substitution-Permutation Network，SP Network）的思想，这是现代分组加密的基础。

1973 年，Feistel 提出使用乘积密码的概念逼近理想分组密码。

混淆

英文 Confusion ，在加密算法中，明文、密文、密钥之间的关系要足够复杂，防止统计分析攻击。

扩散

英文 Diffusion ，明文或密钥的每一比特的变化尽可能多地影响到输出密文序列的变化，以便隐蔽明文的统计特征。

乘积密码

依次使用两个或两个以上的基本密码，所得结果的密码强度高于所有单个密码强度。

迭代结构

常用 Feistel 网络，优点如下：

  1. 加解密的相似性
  2. 物理上的重复性易于在软硬件上实现

加密算法 Encryption ：

解密算法 Decryption：

加解密过程唯一的不同：子密钥的使用顺序。

特点：雪崩效应（输入明文或密钥即使只有很小的变化，也会导致输出密文产生巨大的变化）。

DES

分组长度 64 比特，密钥长度 64 比特（其中有效长度为 56 比特），其中 8 的倍数位为奇校验位（保证每 8 位有奇数个 1）。

基本结构

如图，64 比特的密钥经过置换选择1和循环移位操作可生成 16 个 48 比特的子密钥。明文 $m$ 经过初始置换 $IP$ 后划分为左右两部分（各32 比特），经过 16 轮 Feistel 网络结果（其中最后一轮不做左右交换）再做一次逆置换 $IP^{-1}$ 得到密文 $c$ 。

img

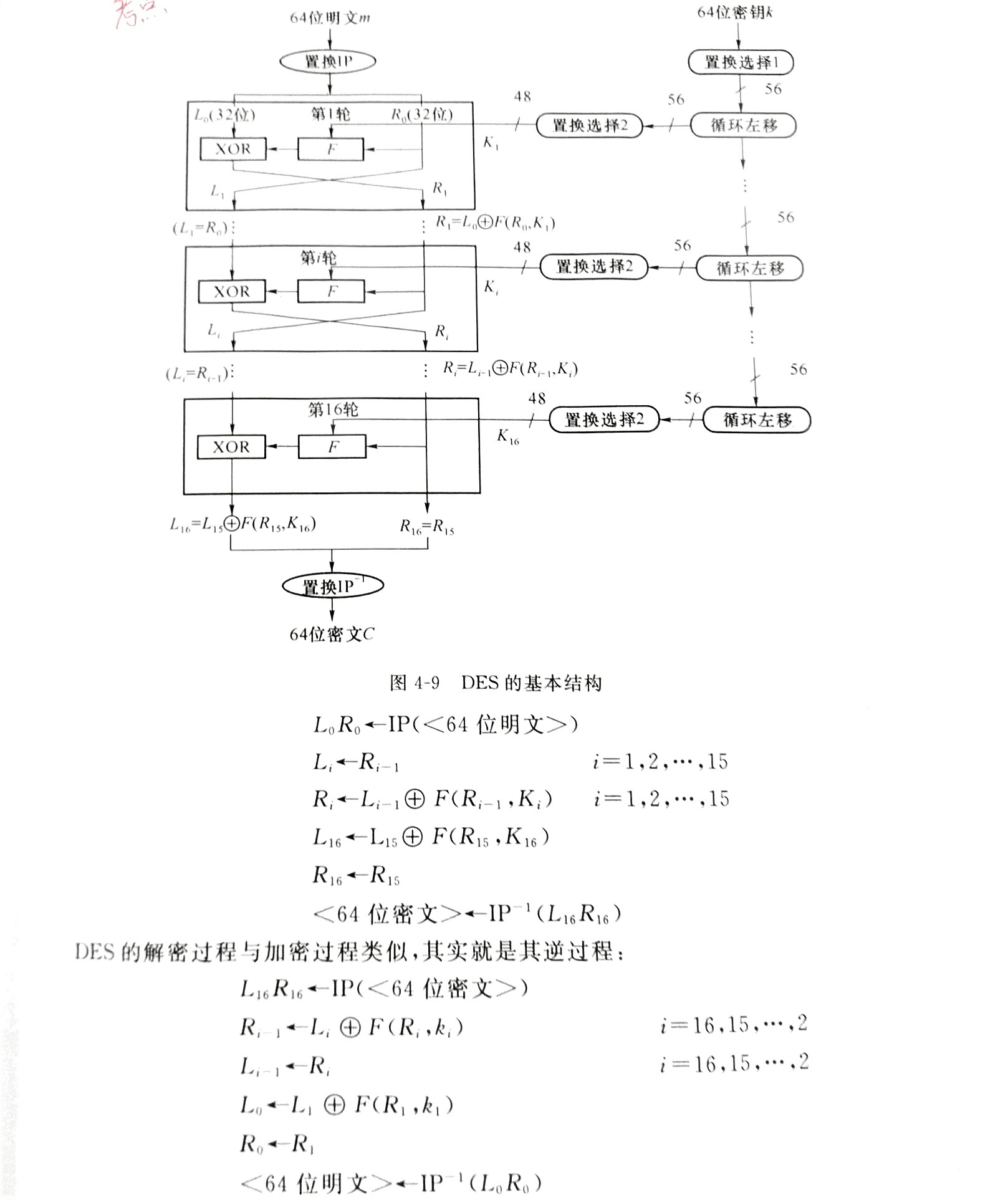
问题：DES 的混淆和扩散体现在哪？（哪个部分起到了这两个作用？）

不妨将 Feistel 网络拆解成代换和置换两个部分，代换起混淆作用，置换起扩散作用。

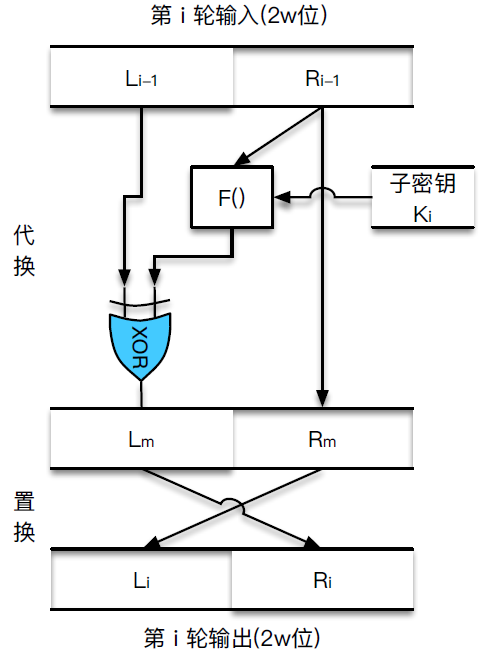
image

密钥编排算法

用于生成迭代的子密钥。具体过程为：

64 位初始密钥经过置换选择1 ( PC-1 ) 后变成 56 位，经过循环左移和置换选择2 ( PC-2 ) 后分别得到 16 个 48 位子密钥 $K_i$ 用做每一轮的迭代运算。

PC-1 去掉了校验位， PC-2 去掉了9, 18, 22, 25, 35, 38, 43, 54 位。

置换选择

置换选择1（PC-1）和置换选择2（PC-2）：

pc1 = (57, 49, 41, 33, 25, 17,  9,
        1, 58, 50, 42, 34, 26, 18,
       10,  2, 59, 51, 43, 35, 27,
       19, 11,  3, 60, 52, 44, 36,
       63, 55, 47, 39, 31, 23, 15,
        7, 62, 54, 46, 38, 30, 22,
       14,  6, 61, 53, 45, 37, 29,
       21, 13,  5, 28, 20, 12,  4)

pc2 = (14, 17, 11, 24,  1,  5,  3, 28,
       15,  6, 21, 10, 23, 19, 12,  4, 
       26,  8, 16,  7, 27, 20, 13,  2, 
       41, 52, 31, 37, 47, 55, 30, 40, 
       51, 45, 33, 48, 44, 49, 39, 56, 
       34, 53, 46, 42, 50, 36, 29, 32)

# Permuted Choice 1 (PC-1) or Permuted Choice 2 (PC-2)
def PermutedChoice(k,num):
    if num == 1:
        t = pc1
    else:
        t = pc2
    ans = "".join(k[x-1] for x in t)
    return ans

循环左移

输入序列经过指定循环左移次数后得到结果（可以使用切片法）：

d = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]
d_1 = [0,-1,-2,-2,-2,-2,-2,-2,-1,-2,-2,-2,-2,-2,-2,-1,-1]

# Loop Left Shift
def LoopLeftShift(s,num):
    l = len(s)
    num %= l
    ans = s[num:]+s[:num]
    return ans

加入取模操作的好处：若 num 为负数，则相当于可以处理循环右移，方便解密时使用。

初始置换 IP 和它的逆置换 IP-1

$IP$ 在第一轮迭代之前进行，目的是将原明文块的位进行换位操作（查表），实际并没有密码意义，因此在软件中时常直接被去掉。

$IP^{-1}$ 在最后一轮迭代之后进行，在加密算法中输出为密文，在解密算法中输出明文，若 $IP$ 被去掉，$IP^{-1}$ 也相应地被去掉。

img

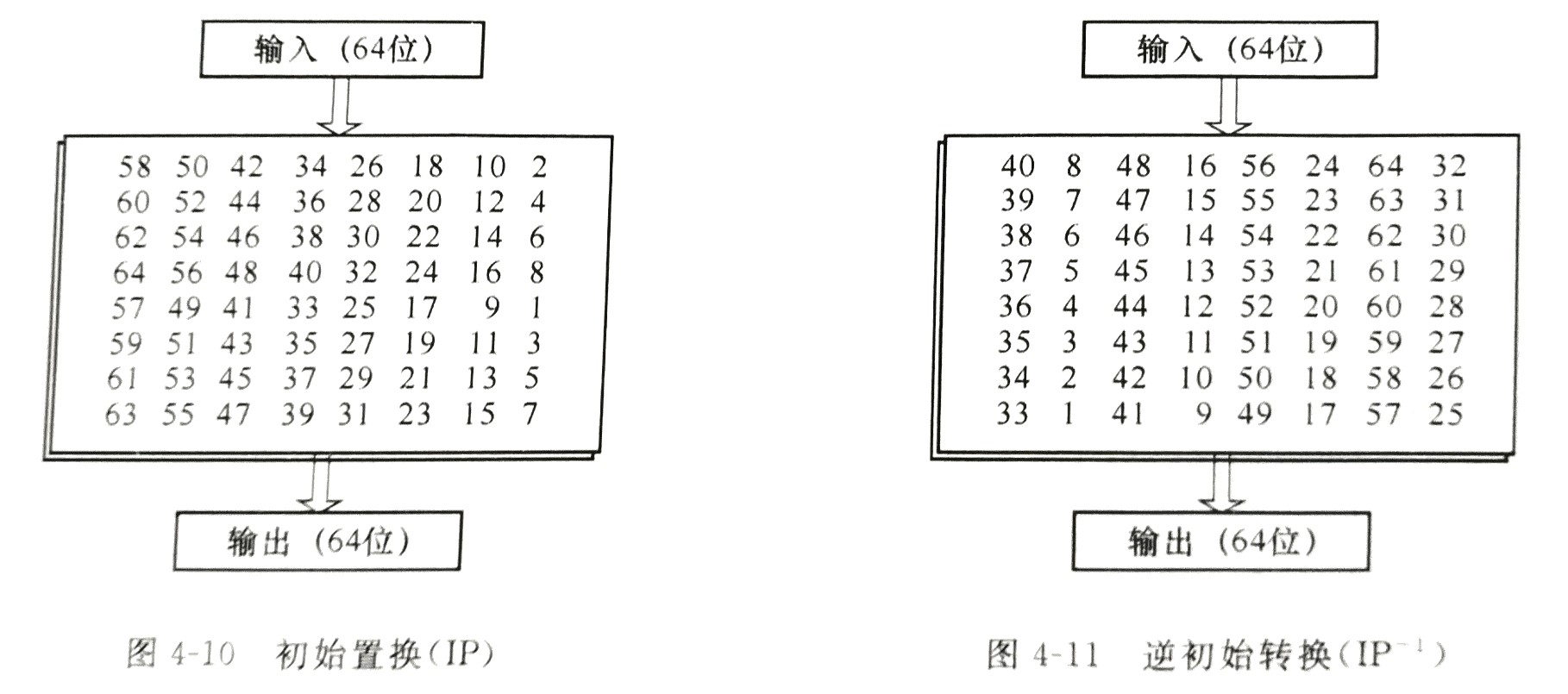
$IP$ 的最后一列为 2, 4, 6, 8, 1, 3, 5, 7，左一列比右一列+8 。

$IP^{-1}$ 的第二列为 8, 7, 6, 5, 4, 3, 2, 1，右边第二列比当前列+8 。

ip =  (58, 50, 42, 34, 26, 18, 10, 2,
       60, 52, 44, 36, 28, 20, 12, 4,
       62, 54, 46, 38, 30, 22, 14, 6,
       64, 56, 48, 40, 32, 24, 16, 8,
       57, 49, 41, 33, 25, 17, 9 , 1,
       59, 51, 43, 35, 27, 19, 11, 3,
       61, 53, 45, 37, 29, 21, 13, 5,
       63, 55, 47, 39, 31, 23, 15, 7)

ip_1 = (40, 8, 48, 16, 56, 24, 64, 32,
        39, 7, 47, 15, 55, 23, 63, 31,
        38, 6, 46, 14, 54, 22, 62, 30,
        37, 5, 45, 13, 53, 21, 61, 29,
        36, 4, 44, 12, 52, 20, 60, 28,
        35, 3, 43, 11, 51, 19, 59, 27,
        34, 2, 42, 10, 50, 18, 58, 26,
        33, 1, 41,  9, 49, 17, 57, 25)

# Initial Permutation, IP
# It has no cryptographic significance
def InitialPermutation(m,inv=False):
    if inv == False:
        t = ip
    else:
        t = ip_1
    ans = "".join(m[x-1] for x in t)
    return ans

F 函数

小小的 F 函数竟然如此复杂。

也称轮函数，包括四个过程：

  1. 扩展置换 ( E 盒 )
  2. 密钥加
  3. S 盒
  4. P 盒

下面，我们分别解释这几个过程。

1. 扩展置换

32 bit → 48 bit

通过扩展置换，数据的右半部分 $R_i$ 从 32 位扩展到 48 位。扩展置换改变了位的次序，重复了某些位。

img

目的：让明文的 1 位可能影响到密文的 2 位，从而快速实现了雪崩效应。（结合 S 盒）

e  = (32, 1,  2,  3,  4,  5,  4,  5, 
       6, 7,  8,  9,  8,  9, 10, 11, 
      12,13, 12, 13, 14, 15, 16, 17,
      16,17, 18, 19, 20, 21, 20, 21,
      22, 23, 24, 25,24, 25, 26, 27,
      28, 29,28, 29, 30, 31, 32,  1)

# Expansion
# the 32-bit half-block is expanded to 48 bits
def Expansion(m):
    ans = "".join(m[x-1] for x in e)
    return ans

2. 密钥加

48 bit ⊕ 48 bit → 48 bit

E 盒输出与子密钥 Xor （逐位异或）。

Python 中，异或使用 ^ 运算符。因为我的处理方法是把字符转成对应的二进制（简单粗暴），所以我写了个封装 Xor 的函数：

# Xor for two str
def Xor(a,b):
    num = len(a)
    ans = "".join(str(int(a[i])^int(b[i])) for i in range(num))
    return ans

3. 代换盒（S 盒）

48 bit → 32 bit

目的是实现非线性代换，是 DES 中的唯一的非线性部分。

实际上是查表运算，8 个 S 盒对应把 48 位分成 8 个组（6 位一组）。

每个 S 盒的输入为 6 位，输出为 4 位。

image

头尾作为行号，中间作为列号。

注意：行号、列号都是从 0 开始的。输出也要写成二进制。

s = [ [[14, 4, 13,  1,  2, 15, 11,  8,  3, 10,  6, 12,  5,  9,  0,  7],
     [0, 15,  7,  4, 14,  2, 13,  1, 10,  6, 12, 11,  9,  5,  3,  8],
     [4,  1, 14,  8, 13,  6,  2, 11, 15, 12,  9,  7,  3, 10,  5,  0],    
     [15, 12,  8,  2,  4,  9,  1,  7,  5, 11,  3, 14, 10,  0,  6, 13]],

     [[15,  1,  8, 14,  6, 11,  3,  4,  9,  7,  2, 13, 12,  0,  5, 10],     
     [3, 13,  4,  7, 15,  2,  8, 14, 12,  0,  1, 10,  6,  9, 11,  5],     
     [0, 14,  7, 11, 10,  4, 13,  1,  5,  8, 12,  6,  9,  3,  2, 15],     
     [13,  8, 10,  1,  3, 15,  4,  2, 11,  6,  7, 12,  0,  5, 14,  9]],

     [[10,  0,  9, 14,  6,  3, 15,  5,  1, 13, 12,  7, 11,  4,  2,  8],     
     [13,  7,  0,  9,  3,  4,  6, 10,  2,  8,  5, 14, 12, 11, 15,  1],   
     [13,  6,  4,  9,  8, 15,  3,  0, 11,  1,  2, 12,  5, 10, 14,  7],     
     [1, 10, 13,  0,  6,  9,  8,  7,  4, 15, 14,  3, 11,  5,  2, 12]],

    [[7, 13, 14,  3,  0,  6,  9, 10,  1,  2,  8,  5, 11,  12,  4, 15],     
     [13,  8, 11,  5,  6, 15,  0,  3,  4,  7,  2, 12,  1, 10, 14,9],     
     [10,  6,  9,  0, 12, 11,  7, 13, 15,  1,  3, 14,  5,  2,  8,  4],     
     [3, 15,  0,  6, 10,  1, 13,  8,  9,  4,  5, 11, 12,  7,  2, 14]],


    [[2, 12,  4,  1,  7, 10, 11,  6,  8,  5,  3, 15, 13,  0, 14,  9],     
     [14, 11,  2, 12,  4,  7, 13,  1,  5,  0, 15, 10,  3,  9,  8,  6],     
     [4,  2,  1, 11, 10, 13,  7,  8, 15,  9, 12,  5,  6,  3,  0, 14],     
     [11,  8, 12,  7,  1, 14,  2, 13,  6, 15,  0,  9, 10,  4,  5,  3]],

    [[12,  1, 10, 15,  9,  2,  6,  8,  0, 13,  3,  4, 14,  7,  5, 11],
     [10, 15,  4,  2,  7, 12,  9,  5,  6,  1, 13, 14,  0, 11,  3,  8],     
     [9, 14, 15,  5,  2,  8, 12,  3,  7,  0,  4, 10,  1, 13, 11,  6],     
     [4,  3,  2, 12,  9,  5, 15, 10, 11, 14,  1,  7,  6,  0,  8, 13]],

    [[4, 11,  2, 14, 15,  0,  8, 13,  3, 12,  9,  7,  5, 10,  6,  1],     
     [13,  0, 11,  7,  4,  9,  1, 10, 14,  3,  5, 12,  2, 15,  8,  6],     
     [1,  4, 11, 13, 12,  3,  7, 14, 10, 15,  6,  8,  0,  5,  9,  2],     
     [6, 11, 13,  8,  1,  4, 10,  7,  9,  5,  0, 15, 14,  2,  3, 12]],

   [[13,  2,  8,  4,  6, 15, 11,  1, 10,  9,  3, 14,  5,  0, 12,  7],     
     [1, 15, 13,  8, 10,  3,  7,  4, 12,  5,  6, 11,  0, 14,  9,  2],     
     [7, 11,  4,  1,  9, 12, 14,  2,  0,  6, 10, 13, 15,  3,  5,  8],     
     [2,  1, 14,  7,  4, 10,  8, 13, 15, 12,  9,  0,  3,  5,  6, 11]]]

问题：为什么一定需要非线性变换呢？

更好地抵抗线性分析（密码分析学中的一种常见分析方法）！

4. 置换盒（P 盒）

32 bit → 32 bit

简单置换。

p = (16,  7, 20, 21, 29, 12, 28, 17,
      1, 15, 23, 26,  5, 18, 31, 10, 
      2,  8, 24, 14, 32, 27,  3,  9,
     19, 13, 30,  6, 22, 11,  4, 25)

运行结果

加密（输出十六进制）

img

加密（输出 Base64 编码）

img

解密（输入十六进制）

img

解密（输入 Base64 编码）

img

安全性

img

多重 DES

img

编程中遇到的问题

若明文长度不是 64 的倍数

加密时经常遇到这种情况，最后一个分组不一定能刚好是 64 比特。

通过搜索引擎查了下，发现有好多种 Padding ，在这里，为了简化，我们统一按字符数若不是 8 的倍数则填充 0x00 补到 8 的倍数。

关键代码：

lm = len(m)
# 若不是8的倍数，则用0x00填充
lm_mod = lm%8
if lm_mod != 0:
    FillLength = 8-lm_mod
    m += FillLength*"\x00"
    lm += FillLength

值得思考的问题

Q: DES 的算法和 S-box 的设计标准未公开。为什么要这样设计呢？

A: 我也不知道啊。

Q: Feistel 密码的设计原则有一项为：简化分析难度。为什么？

A: 设计越复杂，越容易出错。做同样的事情，越简单越好。

没有什么是不朽的，包括艺术本身。

唯一不朽的，是艺术所传递出来的对人和世界的理解。

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自 ComyDream 。
本文链接：http://comydream.github.io/2018/12/29/cryptography-des/

Powered by Hexo
Theme - Material