密码学中的数论 | ComyDream Studio

密码学中的数论

source. 12月 16, 2020

一群人找呀找，突然发现：最初等的数论很适合用于设计密码。

基础概念

整除

$b\mid a$ 表示 $b$ 整除 $a$，其中 $b$ 是 $a$ 的因数，$a$ 是 $b$ 的倍数。

整除符号 $\mid$ 可使用 LaTeX 代码 \mid 。

性质：

若 $a\mid 1$，则 $a=\pm 1$
若 $a\mid b$ 且 $b\mid a$，则 $a=\pm b$
若 $b\ne 0$，则 $b\mid 0$，即 $0$ 是所有非零数的倍数
若 $a\mid b$ 且 $b\mid c$，则 $a\mid c$（传递性）
对任意整数 $m,n$，若 $b\mid g$ 且 $b \mid h$，则可得出 $b\mid (mg+nh)$

素数、算数基本定理

整数 $p>1$ 是素数，当且仅当它只有因子 $\pm 1$ 和 $\pm p$（通常忽略负数，即它的因子只有 $1$ 和它本身）。

算术基本定理：任意整数 $a>1$ 都可以唯一分解成下面形式：

$a=p_1^{\alpha_1}\times p_2^{\alpha_2}\times \cdots\times p_t^{\alpha_t}$

其中，$p_1,p_2,\dots,p_t$ 均为素数，且 $p_1<p_2<\dots,p_t$ ，所有 $\alpha_i$ 均为正整数。

最大公因数、互素、欧几里得算法

$a$ 和 $b$ 的最大公因数是能同时整除 $a$ 和 $b$ 的最大整数，记为 $\gcd(a,b)$ 。

$\gcd(b,0)=b$

在数论语境下可以省略 $\gcd$，直接将最大公因数记为 $(a,b)$ 的形式。

两个整数 $a$ 和 $b$ 是互素的，当且仅当它们只有一个正整数公因子 $1$ ，即 $\gcd(a,b)=1$ 。

求最大公因数常用欧几里得算法：

若 $a\bmod b=0$，则 $\gcd(a,b)=b$
当 $a\bmod b\ne 0$，则递归计算 $\gcd(a,b)=\gcd(b,a\bmod b)$

Python 代码：

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a%b)

随机数互素概率

两个随机数互素的概率约为 $0.6$ 。

推导如下。

令 $P=\Pr\left[\gcd(a,b)=1 \right]$ 。

任取两个随机数 $a$ 和 $b$，设 $\gcd(a,b)=d$ ，可以做如下等价变换。

$\gcd(a,b)=d\Leftrightarrow\begin{cases} d\mid a\\ d\mid b\\ \gcd(\frac{a}{d},\frac{b}{d})=1 \end{cases}$

在所有整数中随机选取一个数 $n$，满足 $d\mid n$ 的概率为 $1/d$ 。则：

$\begin{align} &\Pr\left[\gcd(a,b)=d \right]\\ =&\Pr\left[d\mid a \right]\cdot \Pr\left[d\mid b \right]\cdot \Pr\left[\gcd(\frac{a}{d},\frac{b}{d})=1 \right]\\ =&\frac{1}{d}\cdot \frac{1}{d}\cdot P\\ =&\frac{P}{d^{2}} \end{align}$

$d$ 可取任意正整数，将所有情况的概率加起来应为 1，有：

$\sum_{d\ge1}\Pr\left[\gcd(a,b)=d \right]=\sum_{d\ge 1}\frac{P}{d^2}=P\sum_{d\ge 1}\frac{1}{d^2}=1$

而有以下恒等式结论可用：

$\sum_{i=1}^{\infty}\frac{1}{t^{2}}=\frac{\pi^2}{6}$

所以：

$P=\frac{6}{\pi^2}\approx0.608$

模运算、同余

定义比 $n$ 小的非负数集合为 $\mathbb{Z}_n=\left\{0,1,\dots,(n-1) \right\}$，称为模 $n$ 的完全剩余系（简称完系）。它的每一个元素代表一个剩余类。

整数集 $\mathbb{Z}$ 的 LaTeX 代码为 \mathbb{Z}。

同余与整除：若 $n\mid (a-b)$，则 $a\equiv b\pmod{n}$

模运算性质：

$\left[(a\bmod n)+(b\bmod n) \right]\bmod n=(a+b)\bmod n$
$\left[(a\bmod n)\times (b\bmod n) \right]\bmod n=(a\times b)\bmod n$

同余式中的模的 LaTeX 代码为 \pmod{n}，模运算的 LaTeX 代码为 \bmod 。

费马小定理

Fermat’s little theorem

若 $a$ 是一个整数，$p$ 是一个素数，那么：

$a^p\equiv a\pmod{p}$

若 $a$ 不是 $p$ 的倍数，即满足 $\gcd(a,p)=1$，那么：

$a^{p-1}\equiv 1\pmod{p}$

欧拉函数

Euler’s totient function

欧拉函数 $\varphi(n)$ 是小于等于 $n$ 的正整数中，与 $n$ 互素的数的个数。

希腊字母 $\varphi$ 读作 phi ，LaTeX 代码为 \varphi 。

$\varphi(1) = 1$
若 $p$ 为素数，则 $\varphi(p)=p-1$
若 $p$ 为素数，则 $\varphi(p^\alpha)=p^\alpha-p^{\alpha-1}$
若 $\gcd(m,n)=1$，则 $\varphi(m\times n)=\varphi(m)\times\varphi(n)$

一般公式：

若 $n=p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}$，
则 $\varphi(n)=\prod_{i=1}^{r} p_{i}^{k_{i}-1}\left(p_{i}-1\right)$ 。

推导：

欧拉函数 $\varphi(n)$ 是小于等于 $n$ 的正整数中，与 $n$ 互素的数的个数。
若 $n=1$，小于等于它的正整数只有 $1$，且 $\gcd(1,1)=1$，所以 $\varphi(1)=1$。
若 $n$ 为素数，因为 $n$ 与小于它的任何正整数都是互素的，所以 $\varphi(n)=n-1$。
若 $n=p^k$，其中 $p$ 为素数，此时当一个数不是 $p$ 的倍数时，它与 $n$ 互素。$[1,n]$ 中共有 $n=p^k$ 个正整数，其中 $p$ 的倍数有 $p,2\cdot p,\dots,p^{k-1}\cdot p$，共 $p^{k-1}$ 个，所以 $\varphi(n)=p^k-p^{k-1}=p^{k-1}(p-1)$。
若 $\gcd(m,n)=1$，根据 CRT，$\mathbb{Z}_{m\times n}^{\ast}$ 和 $\mathbb{Z}_m^{\ast}\times \mathbb{Z}_n^{\ast}$ 构成一一映射，所以 $\varphi(m\times n)=\varphi(m)\times \varphi(n)$。

所以，对于 $n=p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}$，其中 $p_1,p_2,\dots p_r$ 为互不相同的素数，由以上推导可知：

$\varphi(n)=\prod_{i=1}^{r} p_{i}^{k_{i}-1}\left(p_{i}-1\right)$

实际上就是 $n$ 的简化剩余系（也称既约剩余系或缩系，reduced residue system，符号为 $\mathbb{Z}_n^{\ast}$）中的元素个数。

欧拉定理

Euler’s theorem

若正整数 $n,a$ 互素（即 $\gcd(n,a)=1$），那么：

$a^{\varphi(n)}\equiv 1\pmod n$

其中，$\varphi(n)$ 为欧拉函数。

素性检验

常用 Miller-Rabin 算法。

米勒-拉宾素性检验 - 维基百科

两个基础理论：

费马小定理：若 $p$ 为素数，且 $\gcd(a,p)=1$，则 $a^{p-1}\equiv 1\pmod{p}$ 。
二次探测定理：若 $p$ 是一个素数，$0<x<p$，则方程 $x^2\equiv 1\pmod{p}$ 的解为 $x\equiv 1\pmod p$ 或 $x\equiv p-1\pmod{p}$ 。

二次探测定理的证明

$\begin{align}x^2&\equiv 1\pmod{p}\\(x+1)(x-1)&\equiv 0\pmod{p}\\p&\mid (x+1)(x-1)\end{align}$

若 $p$ 为素数，那么 $p$ 不可被拆分为几个素数的乘积，有 $p\mid (x+1)$ 或 $p\mid (x-1)$ 成立。所以 $x\equiv 1\pmod{p}$ 或 $x\equiv p-1\pmod{p}$ 。

若 $p$ 不是素数，则不一定成立（可能因数会被拆到两项中）。

Miller-Rabin 算法

要测试一个奇数 $n\ge 3$ 是否为素数，可将 $n-1$ 表示为：

$n-1=2^s\cdot d$

其中，$s$ 和 $d$ 都是正整数，且 $d$ 是奇数。

在每次测试开始时，随机选一个整数 $a$ ，$1<a<n-1$。

若满足以下条件的一种，则判定 $n$ 有可能是素数：

$\begin{align} a^d&\equiv 1\pmod{n}\\ a^{2^rd}&\equiv n -1\pmod{n} \end{align}$

其中，$r=0,~1,\dots,~s-1$。（注意：只要其中有一个 $r$ 使得第二个式子成立，则判定 $n$ 有可能是素数）

Q: 你说它有可能是素数，具体的概率是多大？

A: 通过一次测试，判定待测数为有可能是素数的概率是小于 $1/4$ 的，那么通过 $t$ 次测试（$a$ 取不同值）都判定为有可能是素数的概率是小于 $(1/4)^t$ 的。因此，通过多次测试，则有很大把握说 $n$ 是素数（$n$ 有不可忽略的概率为素数）。

原理

将 $n-1$ 分解为 $2^sd$，其中 $d$ 为奇数。

根据费马小定理，若 $n$ 为素数，则 $a^{n-1}\equiv a^{2^sd} \equiv 1\pmod{n}$ 成立。

根据二次探测定理，若 $n$ 为素数，则对于以下数列：

$a^d,a^{2d},\dots a^{2^{s-1}d},a^{2^sd}\pmod{n}$

最后一个数要为 $1$，且每一个数都是前一个数的平方（对 $n$ 取模），因此下面两条必有一条是正确的：

数列的第一个数为 $1$，那么其后的所有数都为 $1$。
数列中（$a^{2^s d}$之前）有一数为 $n-1$，那么其后的所有数都为 $1$。（因为 $-1$ 的平方是 $1$）

Q: 直接检测 $a^{2^s d}\bmod n=1$ 是否成立不香吗？干嘛还要这么麻烦？

A: 少年，我们要的是效率！你想想看是不是计算低次幂比高次幂更快。事实上，一般要计算高次幂，为了提高效率也是先计算低次幂。

伪代码

MR(n)
    分解n-1 = 2^{s}d
    随机选择整数a (1<a<n-1)
    if a^{d} mod n = 1
        return 有可能是素数
    for j = 0 to s-1
        if a^{2^{j}d} mod n = n-1
            return 有可能是素数
    return 是合数

例子：判断29是不是素数

对于一个素数 $n=29$，有 $n-1=28=2^2\cdot 7=2^s d$，得到 $s=2,~d=7$ 。

第一次测试，选择一个数 $a=10$ 。

计算 $10^7\bmod 29=17$，既不为 $1$ 也不为 $28$ 。

计算$(10^7)^2\bmod 29=28$，因此返回「有可能是素数」。

第二次测试，选择一个数 $a=2$ 。

计算 $2^7\bmod 29=12$，既不为 $1$ 也不为 $28$ 。

计算 $(2^7)^2\bmod 29=28$，因此返回「有可能是素数」。

扩展欧几里得算法

Extended Euclidean algorithm

用于求有限域上的乘法逆元。

直接上实例，原理如下：

为了方便计算和书写，通常写为表格：

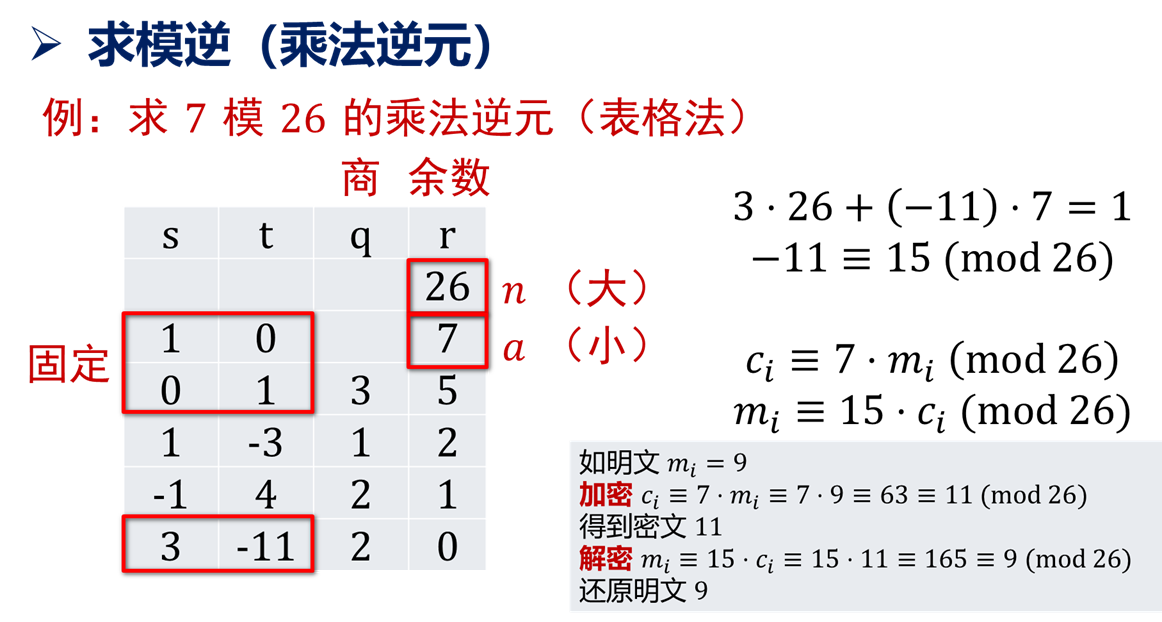
可以试试例题：

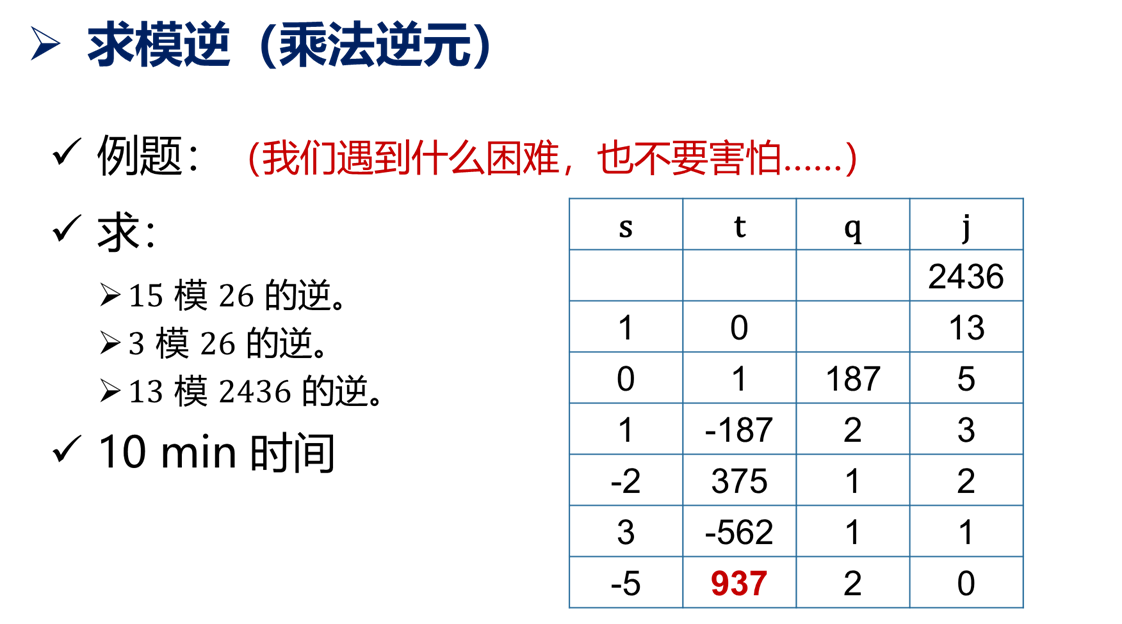
计算复杂度：$O(\log^3 n)$

Python 3.8+ 原生支持求模逆：

pow(9, -1, 29)

要求 $\operatorname{GF}(2^m)$ 上的乘法逆元式，稍微复杂点。不过其实只是把数换为多项式了。

题干会给出一个不可约的模式 $m(x)$ 。

注意，运算过程中所有系数都是在 $\operatorname{GF}(2)$ 上的，即只能取 0 或 1 。

中国剩余定理

Chinese Remainder Theorem, CRT

也叫孙子定理。

有一同余方程组：

$\left\{ \begin{matrix} x \equiv b_1 \pmod {m_1} \\ x \equiv b_2 \pmod {m_2} \\ \vdots \qquad\qquad\qquad \\ x \equiv b_n \pmod {m_n} \end{matrix} \right.$

有解的条件：（模数两两互素）若模数 $m_1,~m_2,\dots,~m_n$ 两两互素，则该同余方程组有解。

Q: 不满足两两互素怎么办？

A: 想办法让它们两两互素！

令 $M$ 为所有模数的乘积，即 $M=m_1\times m_2\times\cdots\times m_n$，设 $M_i=M/m_i$。

设 $M_i^{\prime}$ 为 $M_i$ 模 $m_i$ 的乘法逆元，即$M_i^{\prime}=(M_i^{-1}\bmod m_i)$。

在模 $M$ 的意义下，方程组只有一个解：

$x\equiv \sum_{i=1}^{n}M_i M_i^{\prime}b_i \pmod{M}$

注意，最后解出来是在模 $M$ 的意义下！

CRT 可用于提升 RSA 解密速度（提升 4 倍左右），因为解密指数 $d$ 通常很大，要计算 $m=c^d\bmod n$，可以把模数 $n$ 拆为 $p\times q$，结合欧拉定理可以较快计算 $c^d\bmod p$ 和 $c^d\bmod p$，然后 CRT 回去就是 $m$ 了。

CRT 可用于带门限的秘密共享方案。

原根、离散对数问题

Primitive root modulo $n$

原根、生成元、本原根，都是一个意思。

若一个数的阶为 $\varphi(n)$，则称它为 $n$ 的本原根。

群内一个元素 $a$ 的阶是使得 $a^{m}=\mathrm{e}$ 成立的最小正整数 $m$，其中 $\mathrm{e}$ 为这个群的单位元。

若 $a$ 是 $n$ 的本原根，则模 $n$ 下 $a$ 的 $1$ 到 $(n-1)$ 各次幂恰能生成 $1$ 到 $(n-1)$ 的每个数，且每个数仅出现一次。

形象地说，假设 $a$ 是 $n$ 的一个本原根，那么：

$a^{1},~a^{2},\dots,~a^{n-1}\pmod{n}$

是：

$1,~2,\dots,~(n-1)$

的一个排列。

因此，模 $n$ 下对任意整数 $b$ 和 $n$ 的本原根 $a$，有唯一的幂 $i$ （$0\le i\le p-1$）使得：

$b\equiv a^{i}\pmod{n}$

那么指数 $i$ 称为以 $a$ 为底（模数为 $n$）的离散对数，记为 $\operatorname{dlog}_{a,n}(b)$ 。

与实数上的对数 $\log$ 相似，显然有以下结论：

$\operatorname{dlog}_{a,n}(1)=0$
$\operatorname{dlog}_{a,n}(a)=1$

由欧拉定理，若 $\gcd(a,n)=1$，则 $a^{\varphi(n)}\equiv1\pmod{n}$ ，不难得出 $a$ 的阶一定为 $\varphi(n)$ 的因数。

所以只需要对 $\varphi(n)$ 的每个真因数 $d$ 验证 $a^d\equiv 1\pmod{n}$ 是否成立即可：

若有一个真因数 $d$ 使上述条件成立，则 $a$ 就不是原根
若都不成立，则 $a$ 是原根

若一个数有原根，则它的所有原根个数为 $\varphi\left(\varphi(n) \right)$ 。

求原根例题：

什么数有原根？只有形如 $2,~4,~p^l$ 或 $2p^l$ 的数才有原根，其中 $p$ 为任意奇素数，$l$ 是正整数。

$34$ 以内的数的原根列表：

$n$	$n$ 的原根	周期 $=\varphi(n)$
2	1	1
3	2	2
4	3	2
5	2, 3	4
6	5	2
7	3, 5	6
9	2, 5	6
10	3, 7	4
11	2, 6, 7, 8	10
13	2, 6, 7, 11	12
14	3, 5	6
17	3, 5, 6, 7, 10, 11, 12, 14	16
18	5, 11	6
19	2, 3, 10, 13, 14, 15	18
22	7, 13, 17, 19	10
23	5, 7, 10, 11, 14, 15, 17, 19, 20, 21	22
25	2, 3, 8, 12, 13, 17, 22, 23	20
26	7, 11, 15, 19	12
27	2, 5, 11, 14, 20, 23	18
29	2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27	28
31	3, 11, 12, 13, 17, 21, 22, 24	30
34	3, 5, 7, 11, 23, 27, 29, 31	16

离散对数表举例：要求以 $2$ 为底，模为 $19$ 的离散对数表。

先打出下表：

$i$	$2^i\bmod 19$
1	2
2	4
3	8
4	16
5	13
6	7
7	14
8	9
9	18
10	17
11	15
12	11
13	3
14	6
15	12
16	5
17	10
18	1

交换两列，以 $a$ 升序排列，可以得到以 $2$ 为底，模为 $19$ 的离散对数表：

$a$	$\operatorname{dlog}_{2,19}(a)$
1	18
2	1
3	13
4	2
5	16
6	14
7	6
8	3
9	8
10	17
11	12
12	15
13	5
14	7
15	11
16	4
17	10
18	9

考虑方程：

$y=g^x\bmod p$

给定 $g,~x$ 和 $p$，可直接计算出 $y$，换句话说，正向过程是容易计算的。

但是，给定 $y,~g$ 和 $p$，计算 $x$ 非常困难，这就是所谓的「离散对数」困难问题。

应用：

Diffie-Hellman
ElGamal

不可约多项式

Irreducible polynomial

多项式中的不可约多项式，相当于正整数中的素数。

系数在 $\operatorname{GF}(2)$ 上且零次项为 1 的不可约多项式有：

$x+1$
$x^{2}+x+1$
$x^3+x^2+1$
$x^3+x+1$
……

由于：

$x^{3}+x^2+x+1=(x+1)(x^2+1)=(x+1)^3\\ x^3+1=(x+1)(x^2+x+1)$

所以，它们两个都是可约多项式。

判断是否可约可以挨个尝试除以比他小的所有（不可约）多项式。

例如：要判断 $x^4+1$ 是否可约，首先除以 $(x+1)$，余式为 $0$，商式为 $(x^3+x^2+x+1)$，所以它为可约多项式。

群、环、域基本概念

群 $\{G,~\cdot\}$

Group

定义一个二元运算 $\cdot$ ，$G$ 中的每一个序偶 $(a,b)$ 通过运算生成 $G$ 中的元素 $(a\cdot b)$，满足下列公理：

[A1] 封闭性：若 $a$ 和 $b$ 都属于 $G$，则 $a\cdot b$ 也属于 $G$
[A2] 结合律：$a\cdot (b\cdot c)=(a\cdot b)\cdot c$
[A3] 单位元：$G$ 中存在元素 $e$，对于 $G$ 中任意元素 $a$，都有 $a\cdot e=e\cdot a=a$ 成立
[A4] 逆元：对于 $G$ 中任意元素 $a$，$G$ 中都存在一个元素 $a^{\prime}$，使得 $a\cdot a^{\prime}=a^{\prime}\cdot a=e$ 成立

如果一个群的元素是有限的，则该群称为有限群，群的阶等于群中元素的个数。

反之，如果一个群的元素是无限的，则该群称为无限群。

若一个群满足交换律，则称它为交换群，或阿贝尔群。