【密码学】Hash 函数之 MD5 算法
Hash 函数是密码学的一个重要分支,是将任意长度的输入变换为固定长度的输出的不可逆的单向密码体制。
下面我们来介绍最著名的 Hash 函数—— MD5 。它是由 MIT 的 Rivest ( RSA 中的 R ) 设计的。MD 是消息摘要 ( Message Digest ) 的意思。该算法把任意长度的消息进行一系列运算最终输出 128 bit (16 字节)的消息摘要(为了方便查看,我们通常用 32 位的十六进制位表示)。
算法过程
该算法实际上都是在二进制表示上的操作,我的处理方法是将字符串先转成二进制组成的字符串,这是一种牺牲内存空间换取编程时间的方法(其实是自己太菜了只会这样写)。
# 将字符串转成二进制字符串
def str2Bin(m):
return "".join('{:08b}'.format(ord(x)) for x in m)
# 调用
m = str2Bin(m)
过程就是简单粗暴地把每个字符转成 8 位的 二进制表示的 ASCII 码。
先说明一下,算法过程中很多都涉及到了神奇的小端序 ( Little Endian ),我也封装了一个简单粗暴的函数,将二进制组成的字符串或十六进制组成的字符串转成小端序:
# 将大端序二进制/十六进制字符串转成小端序
# Hex == True means Hex, Hex == False means Bin
def LittleEndian(s,Hex):
l = len(s)
ans = ""
## 二进制
if Hex == False:
i = l-8
while i >= 0:
ans += s[i:i+8]
i -= 8
## 十六进制
else:
i = l-2
while i >= 0:
ans += s[i:i+2]
i -= 2
return ans
算法中多次使用 模 232 加法,我们也可以把它封装成一个函数,方便以后调用:
# 模2的32次方加
def addMod2_32(a,b):
return (a+b)%(2**32)
1. 附加填充位
填充 1 个 1 和 若干个 0 使得消息长度(包括原始消息的长度和本次填充的长度)模 512 与 448 同余,需要特别注意的是,若原始消息长度刚好满足模 512 与 448 同余,则还需要填充 1 个 1 和 511 个 0 。
我先计算长度模 512 等于多少,然后分三种情况进行操作,过程参看以下代码:
## Padding
lm_mod = lm%512
### 若原始消息长度刚好满足模512与448同余
### 则还需要填充512位
if lm_mod == 448:
FillLength = 512
elif lm_mod > 448:
FillLength = 512+448-lm_mod
else:
FillLength = 448-lm_mod
## 填充
m += '1'+(FillLength-1)*'0'
这样,再将原始长度以 64 比特表示附加在填充结果的后面,从而使得最终的长度(包括原始消息的长度、本次填充的长度和六十四位的消息长度)是 512 比特的倍数。
那么问题来了,64 比特消息长度是怎么样的(正常的消息长度不会超过 264 bit = 231 GB 的请你放心)?是放最前面还是最后面?顺序是怎么样的?
这个问题其实困扰了我很久,导致我虽然实现了后续的过程,但是结果一直是错的,连第一轮的第一步得到的链接变量 B 都是错的。课本上或网上的大部分对算法的讲解都没有提到这个,我后面也是突然想到有这种可能试出来的。
其实它是先把消息长度写成 64 bit ,然后变换成小端序,这个过程我们可以先把消息长度用 bin() 函数转成二进制字符串,然后再用 zfill 函数填充至 64 bit,然后调用我们前面写的转成小端序的函数。
# Padding length
length = LittleEndian(bin(lm%(2**64))[2:].zfill(64),False)
m += length
lm = len(m) # 填充之后的消息长度
2. 初始化链接变量
# Initial Variable A, B, C, D
IV_A = 0x67452301
IV_B = 0xefcdab89
IV_C = 0x98badcfe
IV_D = 0x10325476
你可能会觉得这和课本上的不太一样,其实就是把课本上的变成小端序后的结果。
3. 分组处理
(回想分组密码)MD5 以 512 bit 为分组长度进行分组。每个分组又被分成 16 个 32 bit 的子分组,分别参与每轮的 16 个步骤。
4. 步函数
该算法包括 4 轮,每轮 16 步。先看看步函数是怎么样的:
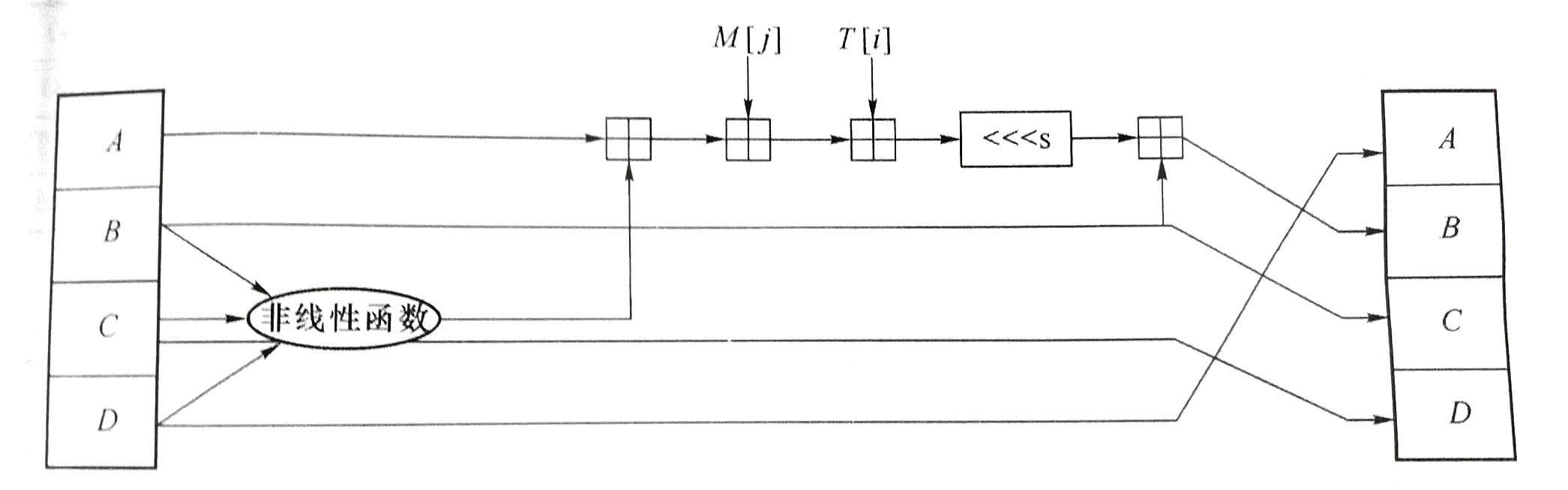
容易看出,上一步的链接变量 D, B, C 直接赋值给下一步的链接变量 A, C, D,相对麻烦的是 B,下面说说它。
为方便起见,后面的加( + )均指 模 232 加法。
A 先和非线性函数的结果加一下,结果再和 M[j] 加一下,结果再和 T[i] 加一下,结果再循环左移 s 次,结果再和原来的 B 加一下,最后的得到新 B。(也是够麻烦的2333)
下面解释下里面涉及到的东西。
非线性函数是啥?
定义如下:
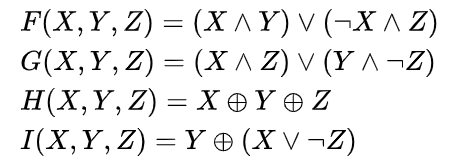
这个用 Python 的 lambda 表达式写起来很简单:
# Nonlinear function
F = lambda x,y,z:((x&y)|((~x)&z))
G = lambda x,y,z:((x&z)|(y&(~z)))
H = lambda x,y,z:(x^y^z)
I = lambda x,y,z:(y^(x|(~z)))
M[j] 是啥?
也就是我们前面说的消息分组的 32 bit 子分组。第一轮中就是简单的 0, 1, …, 15 。
后面三轮的次序由下面置换确定:
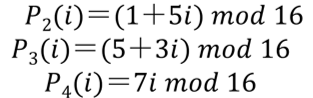
实际上,我们在编程的时候更喜欢把表打出来(牺牲空间换取时间):
# 每次 M[i](消息分片)次序。
M = ((0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15),
(1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12),
(5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2),
(0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9))
因为不用修改,所以可以用元组存储,比列表存储具有更好的时空效率。
T[i] 是啥?
首先明确,T[i] 是常数。
其中 $i$ 为弧度,方框代表取整数部分。
循环左移几位?
这个在算法设计的时候就规定好了,我们可以打表:
# 每次循环左移的位数
Shi = ((7,12,17,22)*4,
(5,9,14,20)*4,
(4,11,16,23)*4,
(6,10,15,21)*4)
有了这些, B 就很容易表示出来。
经过 4×16 次迭代后,我们可以得到最后的链接变量 A, B, C, D,将其分别与初始变量进行下模 232 加法,写成十六进制拼接起来就是 MD5 值了(最后还要分别小端序反转下)!
完整代码
MD5_tables.py
#-*- coding:utf-8 -*-
import math
# Initial Variable A, B, C, D
IV_A = 0x67452301
IV_B = 0xefcdab89
IV_C = 0x98badcfe
IV_D = 0x10325476
# Nonlinear function
F = lambda x,y,z:((x&y)|((~x)&z))
G = lambda x,y,z:((x&z)|(y&(~z)))
H = lambda x,y,z:(x^y^z)
I = lambda x,y,z:(y^(x|(~z)))
# Loop Left Shift
L = lambda x,n:(((x<<n)|(x>>(32-n)))&(0xffffffff))
# 每次循环左移的位数
Shi = ((7,12,17,22)*4,
(5,9,14,20)*4,
(4,11,16,23)*4,
(6,10,15,21)*4)
# 每次 M[i](消息分片)次序。
M = ((0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15),
(1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12),
(5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2),
(0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9))
# 将大端序二进制/十六进制字符串转成小端序
# Hex == True means Hex, Hex == False means Bin
def LittleEndian(s,Hex):
l = len(s)
ans = ""
if Hex == False:
i = l-8
while i >= 0:
ans += s[i:i+8]
i -= 8
else:
i = l-2
while i >= 0:
ans += s[i:i+2]
i -= 2
return ans
# 将字符串转成二进制字符串
def str2Bin(m):
return "".join('{:08b}'.format(ord(x)) for x in m)
# 模2的32次方加
def addMod2_32(a,b):
return (a+b)%(2**32)
# 产生常数T[i],常数有可能超过32位,需要&0xffffffff操作
# 返回的是十进制的数。
def T(i):
result = (int(4294967296*abs(math.sin(i))))&0xffffffff
return result
MD5.py
#-*- coding:utf-8 -*-
# Author: D. Jog Yummy
import math
from MD5_tables import *
# Calculate the MD5 value
def MD5(m):
## str to binstr
m = str2Bin(m)
lm = len(m)
## Padding
lm_mod = lm%512
### 若原始消息长度刚好满足模512与448同余
### 则还需要填充512位
if lm_mod == 448:
FillLength = 512
elif lm_mod > 448:
FillLength = 512+448-lm_mod
else:
FillLength = 448-lm_mod
m += '1'+(FillLength-1)*'0'
# Padding length
length = LittleEndian(bin(lm%(2**64))[2:].zfill(64),False)
m += length
lm = len(m)
## Generate Initial Variable(IV)
A,B,C,D = IV_A,IV_B,IV_C,IV_D
for i in range(0,lm,512):
Y = m[i:i+512]
for j in range(4): # 共4轮
for k in range(16): # 每轮16个步骤
# A, B, C, D Backup
AA,BB,CC,DD = A,B,C,D
## Nonlinear function
if j == 0:
t = F(B,C,D)
elif j == 1:
t = G(B,C,D)
elif j == 2:
t = H(B,C,D)
else:
t = I(B,C,D)
T_i = T(16*j+k+1)
M_j = LittleEndian(Y[M[j][k]*32:M[j][k]*32+32],False)
A, C, D = DD, BB, CC
B = addMod2_32(AA,t)
B = addMod2_32(B,int(M_j,2))
B = addMod2_32(B,T_i)
B = L(B,Shi[j][k])
B = addMod2_32(B,BB)
print str(16*j+k+1).zfill(2),
print hex(A).replace("0x","").replace("L","").zfill(8),
print hex(B).replace("0x","").replace("L","").zfill(8),
print hex(C).replace("0x","").replace("L","").zfill(8),
print hex(D).replace("0x","").replace("L","").zfill(8)
print "*"*38
ans1 = LittleEndian(hex(addMod2_32(A,IV_A))[2:-1],True).zfill(8)
ans2 = LittleEndian(hex(addMod2_32(B,IV_B))[2:-1],True).zfill(8)
ans3 = LittleEndian(hex(addMod2_32(C,IV_C))[2:-1],True).zfill(8)
ans4 = LittleEndian(hex(addMod2_32(D,IV_D))[2:-1],True).zfill(8)
return ans1+ans2+ans3+ans4
def main():
# m = raw_input("Please input the message: ")
m = "iscbupt"
# m = "Beijing University of Posts and Telecommunications"
ans = MD5(m)
print "The MD5 of this message is:\n\t"+MD5(m)+" (Lowercase)\n\t"+ans.upper()+" (Uppercase)"
if __name__ == '__main__':
main()
选择 Python 的原因?
因为写起来简单呀!因为看起来更接近自然语言呀!因为懒啊!
体会
心很累。感觉很多细节教材中都没有提到,这些细节问题老师无法提供帮助,需要自己琢磨。
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2018/12/28/cryptography-md5/