【密码学】数字签名技术和密码协议

source. 12月 24, 2018

快考试了呀QAQ，密码学和 Java 还几乎啥都还不会QAQ。密码学课程设计报告也不想动QAQ，最近真的懒到爆炸，啥事都不想做QAQ。

期末将至，我从今开始复习，至考方休。我将不去浪、不熬夜、不刷剧。我将不看汇编，不做CTF题。我是图书馆的雕像，自习室的幽灵。我是唤醒黎明的号角，闪耀午夜的台灯，守望课本的双眼，追寻知识的灵魂。我将生命与希望献给期末，今夜如此，夜夜皆然。

数字签名技术

在日常生活中，手写签名是传统的用于书信、合同、契约、批复文件等的确认方式，手写签名代表着签名者对文件的认可，愿意承担事后的责任。在网络时代，为了保证网上商务活动的安全，需要一个很重要的安全机制——数字签名。

但他们两者也有显著的区别，手写签名与物理载体（如纸张）一一绑定，而数字签名没有载体，从而需要和消息绑定起来；手写签名由消息接收者用肉眼分辨签名的特征是否相符，容易受主观意识影响，而数字签名依赖于数学算法，结果比较客观。

数字签名大体分为带仲裁的和不带仲裁的两类。

数字签名具有三个特点：不可否认、不可伪造、公正的仲裁。

我们讨论的是不带仲裁的数字签名，这种数字签名主要依赖公钥密码体制来实现。

前提：加密/解密算法顺序可互换。即：D_k(E_z(m)) = E_z(D_k(m)) = m。

签名方案的基本参数有(M, S, K, Sign, Ver)，分别对应消息空间、签名空间、密钥空间、签名算法集合、验证算法集合。

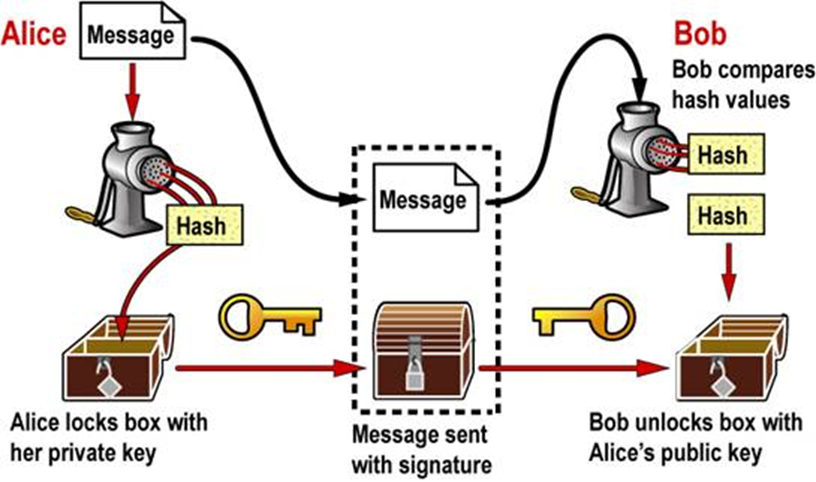
一个完整的数字签名方案包括三个部分：

密钥生成算法：签名者生成 k 和 z，分别代表私钥和公钥；
签名算法：签名者对任意消息用自己的私钥解密；
验证算法：验证者用签名者的公钥对签名值进行加密。

基于RSA的签名方案

让我们一边回顾RSA公钥密码体制以边学习基于它的签名算法吧！

它的安全性基于大整数的因数分解的困难性。

任意生成两个大素数 p 和 q，由他们计算 n = p·q 是容易的，但由 n 分解出 p 和 q 是困难的。

也很容易由 p 和 q 计算出 n 的欧拉函数 φ(n) = (p-1)·(q-1) ，这样，我们选定一个与 φ(n) 互素的数 e 作为加密因子，可由扩展Euclid算法计算出解密因子 d （即私钥），其中 d ≡ e^-1(mod φ(n))。

总结下就是这样：

任意选取两个大素数 p 和 q，

n = p·q

φ(n) = (p-1)·(q-1)

e·d ≡ 1 (mod φ(n))

加密算法：c ≡ m^e (mod n)

解密算法：m ≡ c^d (mod n)

公钥为 (n,e) ，私钥为 d

开始讲解密钥生成、签名与验证算法！

密钥生成算法

与 RSA 密码体制一样，任意选取两个大素数 $p$ 和 $q$，计算 $n = p·q$ 及其欧拉函数 $φ(n) = (p-1)·(q-1)$ ，然后随机选取一个与 $φ(n)$ 互素的数 $e$作为公钥，用扩展Euclid算法计算出私钥 $d ≡ e^{-1}\mod φ(n)$。

签名算法

签名算法对应RSA密码体制中的解密过程。

设待签名的消息为 $m$ ，则签名者A先利用一个安全的Hash函数 $h$ 来产生一个消息摘要 $h(m)$，然后签名者用自己的私钥计算签名 $s ≡ h(m)^d\mod n$ ，将 $(s, m)$ 发送给消息接收者 B。

验证算法

验证算法对应RSA密码体制中的加密过程。

签名接收者 B 收到消息 $m$ 和签名 $s$ 后，先利用 A 使用的Hash函数 $h$ 来产生一个消息摘要 $h(m)$，然后检验同余式 $h(m) ≡ s^e\mod n$ 是否成立。若成立，则说明签名有效，否则签名无效。

安全性

引入Hash函数使得单纯地对消息本身进行签名具有更好的抗攻击性。而且，若攻击者截取一段发往签名者的密文，将其盲化（乘上一个盲化因子 R 的 e 次方）后发送给签名者让其签名，攻击者就能从中计算出密文对应的明文。另外，对于大消息来说，将其映射到固定长度再签名，大大提升了签名的效率。

ElGamal签名方案

它的安全性基于有限域的离散对数问题。

密钥生成算法

选择一个满足安全性要求的大素数 p ，然后选择它的一个原根 g 和随机数 x ，计算 y ≡ g^x (mod p) 。

公钥：(p, g, y) ，私钥：x 。

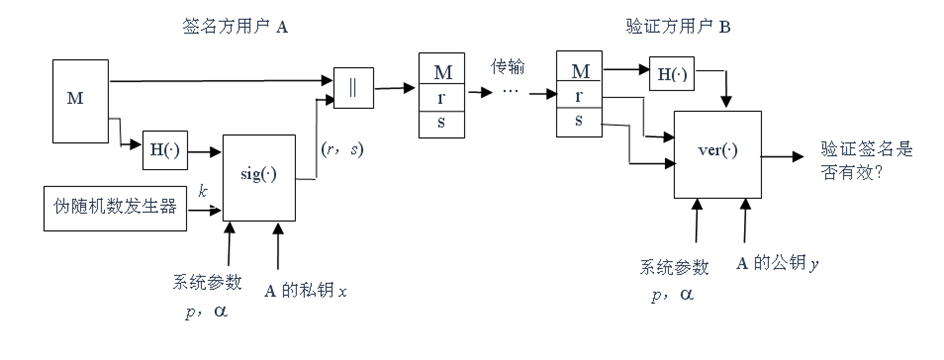
签名算法

设待签名的消息为 m ，签名者首先选择随机数 k ，计算 r ≡ g^k (mod p) ，s ≡ [h(m) - xr]k^-1 (mod (p-1)) ，则对消息的数字签名为 (r, s)。其中，h 为安全的Hash函数。

验证算法

签名接受者接收到消息 m 后，首先计算它的Hash值 h(m)，然后验证同余式 y^r·r^s ≡ g^h(m) (mod p) 是否成立。若成立，则说明签名有效，否则签名无效。

正确性

由 s ≡ [h(m) - xr]k^-1 (mod (p-1)) 可推出 x·r + k·s ≡ h(m) (mod (p-1)) ，进而 y^r·r^s ≡ g^{x·r + k·s} ≡ g^h(m) (mod p) 。

我的理解是：取对数（或者称取指标）模变成原来模的欧拉函数。因为 p 是素数，故 φ(p) = p-1。

安全性

k 不能泄露，且不能重复使用。

Schnorr签名体制

Schnorr签名体制的安全性也是基于有限域的离散对数问题。

密钥生成算法

首先选择一个大素数 p ，再选择一个 p-1 的大素因子 q ，然后选择一个 p 的生成元（原根）g，要求 g^q !≡ 1 (mod p) ，最后选取随机数 x 满足 1 < x < q，计算 y ≡ g^x (mod p) ，则公钥为 (p, q, g, y)，私钥为 x 。

签名算法

签名者选择随机数 k ，1 ≤ k ≤ q-1，然后计算：

r ≡ g^k (mod p)

e ≡ h(m, r)

s ≡ (x·e+k) (mod q)

签名：(e, s)

验证算法

r₁ ≡ g^s·y^-e (mod p)

e = h(m, r₁)

特点

签名速度快、签名长度较短。

密码协议

密码协议是以密码算法为基础的协议，也称作安全协议，它是为了达成某些安全属性而设计的协议。

零知识证明

零知识证明（Zero Knowledge Proof）的一方成为证明者（Prover），另一方成为验证者（Verifier），P 试图在不向 V 提供任何有用的信息的情况下，使 V 相信某个论断是正确的。

通俗来说， V 知道 P 有个秘密，但完全不知道秘密的内容（最小泄露证明）。

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自 ComyDream 。
本文链接：http://comydream.github.io/2018/12/24/cryptography-protocol/