【算法笔记】数论

Author Avatar
source. 10月 25, 2018
  • 在其它设备中阅读本文章

当看不懂代码时，把自己当成计算机，一步一步地算，总会搞清楚的，虽然有时候这种方法很傻……


数论真的太难了Orz。

快速幂

计算 $x^n$ 仅需 $O(\log n)$ 时间。

ll poww(ll x, ll n)
{
    if (x == 0) return 0;
    ll ans = 1;
    while (n)
    {
        if (n & 1) ans *= x;
        x *= x;
        n >>= 1;
    }
    return ans;
}

带模数：

ll poww(ll x, ll n, ll m)
{
    if (x == 0) return 0;
    ll ans = 1;
    x %= m;
    while (n)
    {
        if (n & 1) ans = ans * x % m;
        x = x * x % m;
        n >>= 1;
    }
    return ans;
}

素数

素数（Prime number），又称质数，指在大于 1 的自然数中，除了 1 和该数自身外，无法被其他自然数整除的数（也可定义为只有 1 与该数本身两个正因数的数）。大于 1 的自然数若不是素数，则称之为合数。

1 不是素数：为了确保该定理的唯一性，1 被定义为不是素数，因为在因式分解中可以有任意多个 1（如3、1×3、1×1×3等都是3的有效约数分解）。

试除法

试除法是整数分解算法中最简单和最容易理解的算法。首次出现于意大利数学家斐波那契出版于1202年的著作。

怎么判定一个数 $n$ 是不是素数呢？

最容易想到的思路：

bool isPrime(int n)
{
    if(n == 1) return false;
    for(int i = 2; i*i <= n; i++)
    if(n % i == 0) return false;
    return true;
}

这其实是试除法的思想。

给定一个合数n（这里，n是待分解的正整数），试除法看成是用小于等于 sqrt (n) 的每个素数去试除待分解的整数。如果找到一个数能够整除除尽，这个数就是待分解整数的因子，同时也可以判定 $n$ 不是素数。

实际上，当 $n$ 很大时，$i\times i$ 容易溢出，从而超出最大整数范围，变成一个负数。所以，我们如此改进：

bool isPrime(int n)
{
    if(n == 1) return false;
    int up = int(sqrt(n)+0.5);    //设置变量避免重复计算sqrt(n)和浮点数误差
    for(int i = 2; i <= up; i++)
    if(n % i == 0) return false;
    return true;
}

但是，在程序设计竞赛中，我们一般不采用此方法（因为效率太低）。

素数筛

素数筛法的思想是去除要求范围内所有的合数，剩下的就是素数了，而任何合数都可以表示为素数的乘积，因此如果已知一个数为素数，则它的倍数都为合数。

Eratosthenes 筛法

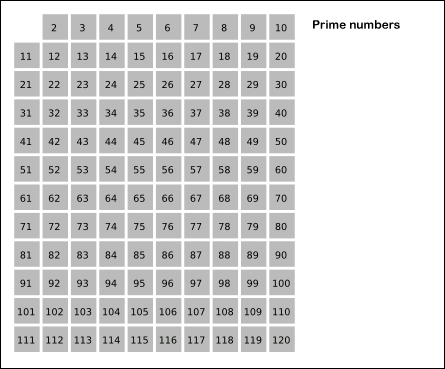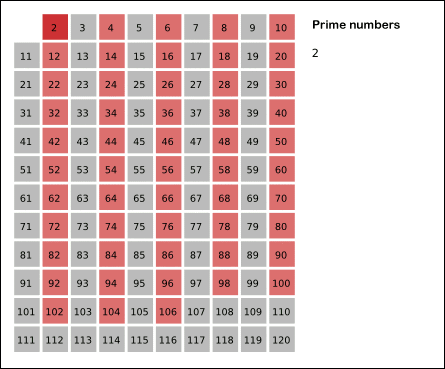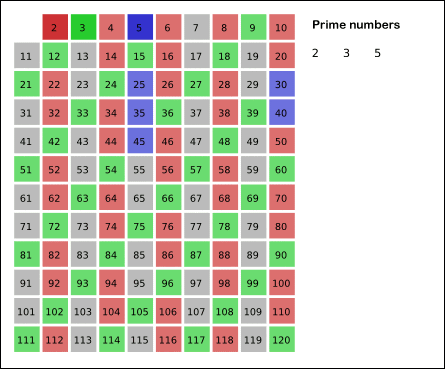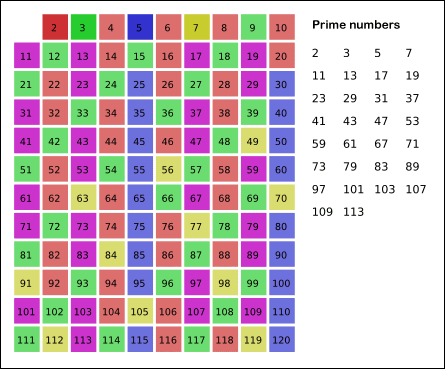
从 $2$ 开始，将每个素数的各个倍数，标记成合数。

先用 $2$ 去筛，即把 $2$ 留下，把 $2$ 的倍数剔除掉；再用下一个素数，也就是 $3$ 筛，把 $3$ 留下，把 $3$ 的倍数剔除掉；接下去用下一个素数 $5$ 筛，把 $5$ 留下，把 $5$ 的倍数剔除掉；不断重复下去……

img

代码如下：

const int maxn = 1e6 + 5;
bool isPrime[maxn];
void erat(int n)
{
    memset(isPrime,-1,sizeof(isPrime));
    isPrime[0] = isPrime[1] = false;    //0和1不是素数
    for(int i = 2; i <= n; i++)
    {
        if(isPrime[i])
        {
            for(int j = i*i; j <= n; j += i)
                isPrime[j] = false;
        }
    }
}

为什么 j 从 i*i 开始？因为 2*i、3*i、……已经被前面 i = 2 的时候、i = 3 的时候……筛过了。

时间复杂度 $O(n\log(\log n))$（实际上已经很小了）。

线性筛法

其实只要会套模板就行。

何为线性筛法？

顾名思义，就是在线性时间，也就是 $O(n)$ 时间内用筛选的方法把素数找出来的一种算法。

在线性时间内求出一个素数表，需要判定是否是素数的时候只要看该数是否在表内就可以瞬间知道是不是素数。

核心原理：每个合数必有一个最大因子（不包括它本身） ，用这个因子把合数筛掉。

还有另一种说法，每个合数必有一个最小素因子，用这个因子筛掉合数。

代码：

const int maxn = 1e6 + 5;
int prime[maxn];    //素数表，保存素数
bool visited[maxn];
int Prime(int n)
{
    int cnt = 0;
    memset(visited,0,sizeof(visited));
    for(int i = 2; i < n; i++)
    {
        if(!visited[i]) prime[cnt++] = i;
        for(int j = 0;j < cnt && i*prime[j] < n; j++)
        {
            visited[i*prime[j]] = 1;
            if(i%prime[j] == 0) break;      //very important
        }
    }
    return cnt;//返回小于n的素数的个数
}

prime数组中的素数是递增的,当i能整除prime[j]，那么i*prime[j+1]这个合数肯定被prime[j]乘以某个数筛掉。
因为i中含有prime[j], prime[j]比prime[j+1]小。接下去的素数同理，所以不用筛下去了。

在满足i%prme[j] == 0这个条件之前以及第一次满足改条件时，prime[j]必定是prime[j]*i的最小因子。

实在是很难理解 Orz。所以说直接套模板就好啦。

img

最大公因数

两个或多个整数的最大公因数（Greatest Common Divisor, gcd）指能够整除这些整数的最大正整数（这些整数不能都为零），一般表示成 $\gcd(a,b)$ 或 $(a,b)$ 。

求解可采用辗转相除法。

代码：

int gcd(int a, int b)
{
    if(a % b == 0) return b;
    return gcd(b, a%b);
}

你也可以直接用STL中的函数 __gcd(a, b)（需要头文件<algorithm>）

互素

互素也叫互质，当且仅当 $gcd(a,b) == 1$ 时，可称 $a$ 和 $b$ 互素。

最小公倍数

两个整数公有的倍数称为它们的公倍数，其中最小的一个正整数称为它们两个的最小公倍数（Lowest Common Multiple, LCM），一般表示成 $lcm(a,b)$ 或 $[a,b]$ 。

有性质：$(a,b)\times[a,b]=a\times b$。

由以上性质可写出代码：

int lcm(int a,int b)
{
    return a/gcd(a,b)*b;    //先做除法防溢出
}

欧拉函数

对正整数 $n$，欧拉函数（Euler’s totient function）是指少于或等于 $n$ 的数中与 $n$ 互质的数的数目。此函数以其首名研究者欧拉命名，通常记为 $\varphi(n)$，也可写成 $\operatorname{phi}(n)$ 。例如：$\varphi(8) = 4$ ，因为 $1,3,5,7$ 和 $8$ 互质。

给出几个定理：

  • $\varphi(1) = 1$

  • 若 $p$ 为素数，则 $\varphi(p)=p-1$

  • 若 $p$ 为素数，则 $\varphi(p^\alpha)=p^\alpha-p^{\alpha-1}$

  • 若 $\gcd(m,n)=1$ ，即 $m$ 与 $n$ 互素，则 $\varphi(m\times n)=\varphi(m)\times\varphi(n)$

一般公式：

  • 若 $n=p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}$，
  • 则 $\varphi(n)=\prod_{i=1}^{r} p_{i}^{k_{i}-1}\left(p_{i}-1\right)=\prod_{p | n} p^{\alpha_{p}-1}(p-1)=n \prod_{p | n}\left(1-\frac{1}{p}\right)$ 。

容易发现，除了 $n=2$ 的情况，其他时候 $\varphi(n)$ 都是偶数。（因为素数除 $2$ 外都是奇数）

举例

代码实现：

求单个欧拉函数：

int phi(int n)
{
    int ans = n;
    int up = int(sqrt(n+0.5));
    for(int i = 2; i <= up; i++)
    {
        if(n%i == 0)
        {
            ans = ans/i*(i-1);
            while(n%i == 0) n/= i;
        }
    }
    if(n > 1) ans = ans/n*(n-1);
    return ans;
}

打表：

const int maxn = 1e6 + 5;
int phi[maxn];
void make_phi(int n)
{
    memset(phi,0,sizeof(phi));
    phi[1] = 1;
    for(int i = 2; i <= n; i++)
    {
        if(!phi[i])
            for(int j = i; j <= n; j += i)
            {
                if(!phi[j]) phi[j] = j;
                phi[j] = phi[j]/i*(i-1);
            }
    }
}

莫比乌斯函数

给出定义：


性质：莫比乌斯函数是积性函数，即有：


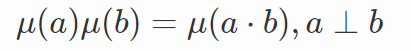
代码实现：

求单个莫比乌斯函数：

int miu(int n)
{
        if(n == 1) return 1;
    int num = 0;
    int up = int(sqrt(n)+0.5);
    for(int i = 2; i <= up; i++)
    {
        if(n%i == 0)
        {
            num++;
            int cnt = 0;
            while(n%i == 0)
            {
                n /= i;
                cnt++;
                if(cnt > 1) return 0;   //存在平方因数
            }
        }
    }
    return (num&1)?1:-1;
}

打表：

const int maxn = 1e6 + 5;
int miu[maxn];
void make_miu(int n)
{
    for(int i = 1; i <= n; i++)
    {
        int target = i == 1?1:0;
        int delta = target - miu[i];
        miu[i] = delta;
        for(int j = i*2; j <= n; j += i)
        miu[j] += delta;
    }
}

莫比乌斯反演

莫比乌斯反演，又称懵逼钨丝繁衍，是一种看了就一脸懵逼的东西。

求模逆

前提：$\gcd(a,m)=1$，即 $a$ 和 $m$ 互素。

模板：

typedef long long ll;
const ll mod = 1e9 + 7;
void exgcd(ll a,ll b,ll& d,ll& x,ll& y)
{
    if(!b) { d = a; x = 1; y = 0; }
    else{ exgcd(b, a%b, d, y, x); y -= x*(a/b); }
}

ll inv(ll a, ll p)
{
    ll d, x, y;
    exgcd(a, p, d, x, y);
    return d == 1 ? (x+p)%p : p-1;
}

本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自 ComyDream 。
本文链接：http://comydream.github.io/2018/10/25/algorithm-num-theory/

Powered by Hexo
Theme - Material