【算法课OJ】实验二
决定程序优雅的是人,而不是语言。
链接:http://192.168.173.163/JudgeOnline/contest.php?cid=1110
密码:123654
问题 A: 最长公共子序列
题目描述
给你一个序列 X 和另一个序列 Z,当 Z 中的所有元素都在X中存在,并且在 X 中的下标顺序是严格递增的,那么就把 Z 叫做 X 的子序列。
例如:Z=
现给你两个序列 X 和 Y,请问它们的最长公共子序列的长度是多少?
输入
输入包含多组测试数据。每组输入占一行,为两个字符串,由若干个空格分隔。每个字符串的长度不超过 100。
输出
对于每组输入,输出两个字符串的最长公共子序列的长度。
样例输入
abcfbc abfcab
programming contest
abcd mnp
样例输出
4
2
0
题意
求“最长公共子序列”最优值,即最长公共子序列的长度。
思路
DP 经典题。
输入两个字符串后,用 la、lb 分别存储 a 数组和 b 数组的长度:
la = strlen(a);lb = strlen(b);
如何 DP ?写一个双层循环,i 从 0 到 la-1,j 从 0 到 lb-1。
状态转移方程:
if(a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1]+1;else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
最后,输出 dp[la][lb] 即可。
代码
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int maxn = 105;
int dp[maxn][maxn];
int main()
{
char a[maxn],b[maxn];
int la,lb;
while(~scanf("%s %s",a,b))
{
la = strlen(a);
lb = strlen(b);
int i,j;
for(i = 0; i < la; i++) dp[i][0] = 0;
for(i = 0; i < lb; i++) dp[0][i] = 0;
for(i = 1; i <= la; i++)
{
for(j = 1; j <= lb; j++)
{
if(a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1]+1;
else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
printf("%d\n",dp[la][lb]);
}
return 0;
}
问题 B: 汽水瓶
题目描述
有这样一道智力题:“某商店规定:三个空汽水瓶可以换一瓶汽水。小张手上有十个空汽水瓶,她最多可以换多少瓶汽水喝?”答案是5瓶,方法如下:先用9个空瓶子换3瓶汽水,喝掉3瓶满的,喝完以后4个空瓶子,用3个再换一瓶,喝掉这瓶满的,这时候剩2个空瓶子。然后你让老板先借给你一瓶汽水,喝掉这瓶满的,喝完以后用3个空瓶子换一瓶满的还给老板。如果小张手上有n个空汽水瓶,最多可以换多少瓶汽水喝?
输入
输入文件最多包含10组测试数据,每个数据占一行,仅包含一个正整数n(1≤n≤100),表示小张手上的空汽水瓶数。n=0表示输入结束,你的程序不应当处理这一行。
输出
对于每组测试数据,输出一行,表示最多可以喝的汽水瓶数。如果一瓶也喝不到,输出 0
样例输入
3
10
81
0
样例输出
1
5
40
题意
一开始给你 n 个空瓶子,然后 3 个空瓶子能换一瓶汽水,问最多可以换多少瓶汽水喝。
注意,当你有 2 个空瓶子的时候,可以先借一瓶。我一开始看到题目没看到后面的就直接交 WA 了 QAQ
思路
因为老师要我讲这题,所以写详细点。
思路一:(常规思路)模拟
ans 存储这一轮完成后的结果,emp 存储这一轮完成后的空瓶数。
题目怎么来,我们就怎么写代码。模拟一下,用 tmp 存储这一轮喝的汽水的瓶数,则有:
ans += tmp;emp = emp % 3 + tmp;
循环的条件是什么?答案很显然是 while(emp >= 2)。
emp == 2 的时候怎么处理?答案是先借一瓶,即 emp++。
最终,输出 ans 即可。
思路二:递归函数
写一个参数是当前空瓶的数量 n 的递归函数,我们就把它叫做 f() 函数吧,考虑三种情况:
- 如果空瓶数为 2 以下(0 或 1),则换不了瓶子,返回 0,结束递归;
- 如果空瓶数为 2,那么可换 1 瓶,返回 1,结束递归;
- 其他情况:本轮可以喝
n/3(除法向下取整),那么本轮之后的空瓶数就是n/3 + n % 3。
那么f()函数的代码就只有三行:
if(n < 2) return 0;if(n == 2) return 1;return n/3 + f(n/3 + n%3);(因为刨除掉了其他情况,所以最后一行可不写if语句)
主函数输出一下f(n)即可。
注意:本题n最多取到100,而且子问题规模下降得很快,所以可以用递归直接写。如果规模很大,后台测试数据量很大,抑或是子问题规模下降得不快的话,可以化递归为递推,也就是开一个数组存储结果,这样避免了重复运算和爆栈。
思路三:找规律
当然了,以上说的都不是最简单的方法。还有一种方法比上面的代码简单多了,在
main()函数中除去return 0;后二至三行代码就能搞定。怎么写呢?先找找规律吧!
先看看样例:
输入 3,输出 1
输入 10,输出 5
输入 81,输出 40
我们其实可以看出输入输出间存在着一种微妙的关系:
输入除 2 向下取整的结果就是输出。
那我们可以自己验证下猜想:
输入 1,输出 0。
输入 2,输出 1。
输入 3,输出 1。
输入 4,输出 2。
输入 5,输出 2。
……
为什么呢?因为有借这种操作。从题目看出,2 个空瓶就可以换 1 瓶汽水,那我们每次拿 2 个空瓶就可以换 1 瓶汽水呗,而且这样还有个好处:每次换不会产生新的空瓶。
代码1(模拟)
#include<iostream>
#include<stdio.h>
using namespace std;
int main()
{
int n;
while(~scanf("%d",&n) && n)
{
int ans = 0,emp = n,tmp;
while(emp >= 2)
{
if(emp == 2) emp++;
tmp = emp/3;
ans += tmp;
emp = emp%3+tmp;
}
printf("%d\n",ans);
}
return 0;
}
代码2(将模拟封装成一个递归函数)
#include<iostream>
#include<stdio.h>
using namespace std;
int f(int n)
{
//如果空瓶数为2以下(0或1),则换不了瓶子,返回0,结束递归
if(n < 2) return 0;
//如果空瓶数为2,那么可换1瓶,返回1,结束递归
if(n == 2) return 1;
return n/3 + f(n/3 + n%3);
}
int main()
{
int n;
while(~scanf("%d",&n) && n)
{
printf("%d\n",f(n));
}
return 0;
}
代码3(找规律)
#include<iostream>
#include<stdio.h>
using namespace std;
int main()
{
int n;
while(~scanf("%d",&n) && n)
{
printf("%d\n",n/2);
}
return 0;
}
问题 C: 矩阵连乘
题目描述
给定 $n$ 个矩阵 $\left\{A_1,A_2,\dots,A_n \right\}$,及 $m$ 个矩阵连乘的表达式,判断每个矩阵连乘表达式是否满足矩阵乘法法则,如果满足,则计算矩阵的最小连乘次数,如果不满足输出 MengMengDa 。
输入
输入数据由多组数据组成(不超过 10 组样例)。每组数据格式如下:
- 第一行是 2 个整数 $n~(1\leqslant n\leqslant 26)$ 和 $m~(1\leqslant m\leqslant 3)$,表示矩阵的个数。
- 接下来 $n$ 行,每行有一个大写字母,表示矩阵的名字,后面有两个整数 $r$ 和 $c$,分别表示该矩阵的行数和列数,其中 $1<r, c<100$。
- 第 $n+1$ 行到第 $n+m$ 行,每行是一个矩阵连乘的表达式($2\leqslant $矩阵个数$\leqslant 100$)。
输出
对于每个矩阵连乘表达式,如果运算不满足矩阵乘法法则的情况(即左矩阵列数与右矩阵的行数不同),则输出 MengMengDa ,否则输出最小矩阵连乘次数。
数据保证结果不超过 1e9 。
样例输入
3 2
A 10 100
B 5 50
C 100 5
ACB
ABC
样例输出
7500
MengMengDa
题意
矩阵连乘题,首先判断是否可连乘,可以则输出最小连乘次数,否则输出 MengMengDa 。
因为这题不要求求最优解,所以代码会稍微简单一点。
思路
先来回顾下我们上课学的矩阵连乘填表方法,不妨把它封装成一个 MatrixChain() 函数。
回忆一下填表的过程,首先,因为如果只有一个矩阵的话,那就不需要乘了,结果肯定是0,于是把对角线全部置为 0。for(int i = 1; i <= n; i++) dp[i][i] = 0;
然后写一个三层循环:
第一层循环
r从2到n,表示连乘矩阵的个数第二层循环
i从1到n-r+1,表示左界下标,那么右界下标j就等于i+r-1- 第三层循环
k从i到j-1,表示隔板位置,这个隔板把原来的问题一分为二
书上的代码把那个表对应的二维矩阵叫做 m[i][j],因为本题输入也叫 m,所以我们就叫它 dp[i][j] 吧。
这样,让 dp[i][j] 中存储 dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j] 的最小值。
先输入 $n$ 个矩阵的名字(单个字符)、行数和列数。这时候我们可以使用 STL 中的 map,这种容器使用红黑树实现,插入、查找、删除的时间复杂度都是 $O(\log n)$;当然也可以使用基于哈希表的 unordered_map,这样插入、查找、删除的时间复杂度都是 $O(1)$;
注意:虽是单个字符,若让 C++ 读入单个字符,可以为 \n,为了避免使用 getchar() 函数,通常使用元素个数为 2 的 char 类型数组存储单个字符。
$m$ 次 query,每次读入一个字符串。令 len = strlen(str),若 len 个矩阵可连乘(对于任意两个连续矩阵,前一个矩阵的列数=后一个矩阵的行数),则输出最小矩阵连乘次数,否则输出 MengMengDa 。
- 首先,不满足矩阵乘法法则的情况好判断,遍历一遍
len个矩阵,若左矩阵列数与右矩阵的行数不同,则直接输出MengMengDa并break; - 若满足矩阵连乘条件,则我们要构造p数组,构造过程参考代码;
- 可以封装一个
void MatrixChain(int p[],int n)函数,用于执行 DP,调用该函数后,结果在dp[1][len]中。
这题我居然 -11!一开始错是因为 RE(运行时错误),开的数组太小。后来 WA(答案错误),几经周折,终于找到了原因。我把如下代码:
MatrixChain(p,len);
printf("%d\n",dp[1][len]);
写成了
MatrixChain(p,n);
printf("%d\n",dp[1][n]);
真是太粗心了!
我还发现很多同学还不会用 STL 中的 map,在算法题中,map 真的很好用,map 就是映射(mapping),也可以视为字典(dictionary),通过它可以建立键(key)值(value)映射。
比如说这题,可以开个结构体叫做 Matrix 用来存储某个矩阵的行数和列数。
假设我想查询A矩阵的行列值,我就可以直接 dir['A'] 。
- 头文件:
#include<map> - 定义:
map<char,int> dir; - 插入:
dir[nam[0]] = tmp; - 查询:
dir[c]
代码
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<map>
using namespace std;
const int maxn = 105;
int dp[maxn][maxn];
void MatrixChain(int p[],int n)
{
for(int i = 1; i <= n; i++) dp[i][i] = 0;
for(int r = 2; r <= n; r++)
{
for(int i = 1; i <= n-r+1; i++)
{
int j = i+r-1;
dp[i][j] = dp[i+1][j]+p[i-1]*p[i]*p[j];
for(int k = i+1; k < j; k++)
{
int t = dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j];
dp[i][j] = min(dp[i][j],t);
}
}
}
}
struct Matrix
{
int r,c;
};
int main()
{
int n,m;
while(~scanf("%d %d",&n,&m))
{
map<char,Matrix> dir;
char nam[8],str[105];
int r,c;
for(int i = 0; i < n; i++)
{
scanf("%s %d %d",nam,&r,&c);
Matrix tmp;
tmp.r = r;
tmp.c = c;
dir[nam[0]] = tmp;
}
for(int cas = 0; cas < m; cas++)
{
scanf("%s",str);
int len = strlen(str);
int p[maxn];
p[0] = dir[str[0]].r;
p[1] = dir[str[0]].c;
bool flag = true;
for(int i = 1; i < len; i++)
{
if(dir[str[i]].r != dir[str[i-1]].c)
{
flag = false;
break;
}
p[i+1] = dir[str[i]].c;
}
if(!flag) puts("MengMengDa");
else
{
MatrixChain(p,len);
printf("%d\n",dp[1][len]);
}
}
}
return 0;
}
问题 D: 01背包问题
题目描述
已知有N种物品和一个可容纳C重量的背包。每种物品i的重量为Wi,价值为Pi。那么,采用怎样的装包方法才会使装入背包物品的总价值最大。
输入
包含多组测试数据。第一行为一个整数T(1<=T<=10),代表测试数据个数。
接下来有T组测试数据。每组测试数据第一行为背包的重量C(C<10000)和物品个数N(N<1000)。接下来的N行分别为物品的重量cost(1<=cost<=100)和价值val(1<=val<=3000000)。(注意:结果可能超过int范围)
输出
对每组测试数据,输出其对应的所装物品的最大价值。
样例输入
1
10 5
2 6
2 3
6 5
5 4
4 6
样例输出
15
题意
如题目描述所示,经典DP题。
思路
先看题目最后的注意,结果可能超过int范围,故采用long long类型。我一般这样写:typefef long long ll;把它“重命名”一下,以后写起来比较简便。
注意在stdio(scanf、printf)中,要写出%lld。
有两种写法(分别对应下面的代码1和代码2).
第一种,也就是书上的这种,m[i][j]代表从第i件物品开始的、在最大容量为j的情况下可以获得的最大收益,最后结果保存在m[1][c];
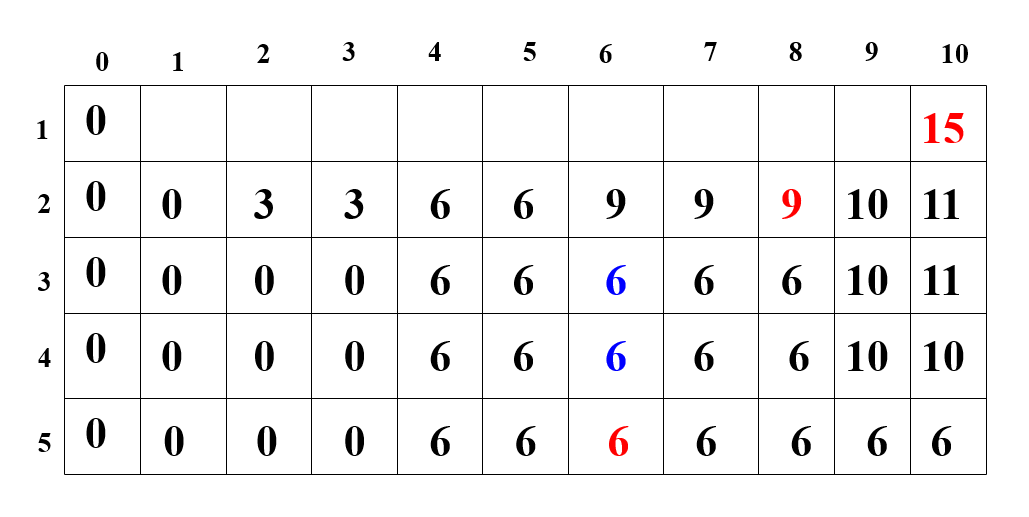
第二种,比较常见的写法,m[i][j]前i件物品、在最大容量为j的情况下可以获得的最大收益,最后结果保存在m[n][c]。
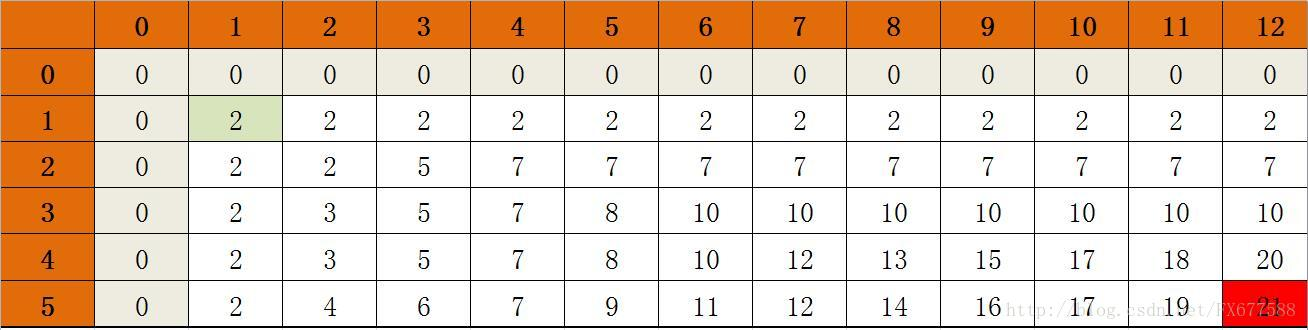
(初始状态)以第二种为例,首先第一行和第一列全置为0,因为
- 0物品,0价值;
- 0容量,0价值。
(状态转移方程)
if (背包体积j小于物品i的体积)
m[i][j] = m[i-1][j]; //背包装不下第i个物体,目前只能靠前i-1个物体装包
else m[i][j] = max(m[i-1][j], m[i-1][j-w[i]] + v[i]);
代码1
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
typedef long long ll;
const int maxn = 1005;
ll m[maxn][maxn];
int main()
{
int t,n;
ll c,w[maxn],v[maxn];
scanf("%d",&t);
while(t--)
{
scanf("%lld %d",&c,&n);
for(int i = 1; i <= n; i++)
scanf("%lld %lld",&w[i],&v[i]);
int i,j,jMax = min(w[n]-1,c);
for(j = 0; j <= jMax; j++) m[n][j] = 0;
for(j = w[n]; j <= c; j++) m[n][j] = v[n];
for(i = n-1; i > 1; i--)
{
jMax = min(w[i]-1,c);
for(j = 0; j <= jMax; j++)m[i][j] = m[i+1][j];
for(j = w[i]; j <= c; j++) m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
m[1][c] = m[2][c];
if(c >= w[1]) m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);
printf("%lld\n",m[1][c]);
}
return 0;
}
代码2
#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e3 + 5;
const int maxc = 1e4 + 5;
const int inf = 0x3f3f3f3f;
ll dp[maxn][maxc];
int main()
{
int t,n;
ll c,w[maxn],v[maxn];
scanf("%d",&t);
while(t--)
{
scanf("%lld %d",&c,&n);
for(int i = 1; i <= n; i++)
scanf("%lld %lld",&w[i],&v[i]);
for(int i = 0; i <= c; i++)
dp[0][i] = 0;
for(int i = 1; i <= n; i++)
dp[i][0] = 0;
for(int i = 1; i <= n; i++)
{
int jMax = min(c,w[i]);
for(int j = 1; j < jMax; j++)
dp[i][j] = dp[i-1][j];
for(int j = w[i]; j <= c; j++)
dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
printf("%lld\n",dp[n][c]);
}
return 0;
}
问题 E: 最大子段和
题目描述
给定n个整数组成的序列a1,a2,…an, 求子段和ai+ai+1+…+aj(子段可为空集)的最大值。
输入
包含多组测试数据。第一行为一个整数T(1<=T<=20),代表测试数据个数。
每组测试数据第一行为一个整数n,代表有n个整数(1<=n<=10000)。
接下来一行有n个数x(-1000<=x<=1000)。
输出
输出其对应的最大子段和。
样例输入
1
6
2 -11 4 13 -1 2
样例输出
18
提示
子段可为空集,答案为0
题意
求最大字段(连续)和。
思路
DP基础题,新开一个b辅助数组,我们这样定义它:b[j]存储选取第j个元素时a[1],...,a[j]的最大子段和。
递归定义b数组(b[0]需初始化为0):
- (前面为正数,有用则要)若
b[j-1] > 0,则b[j] = b[j-1] + a[j]; - (前面为负数,无用则丢)否则
b[j] = a[j]。
则易得出最优值为b数组中的最大值(因为题目要求若为负数则输出0,所以要和0做一次max)。
代码
#include<iostream>
#include<stdio.h>
using namespace std;
const int maxn = 1e4 + 5;
int main()
{
int t,n,a[maxn],b[maxn] = {0};
scanf("%d",&t);
while(t--)
{
int ans = 0;
scanf("%d",&n);
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
if(b[i-1] > 0) b[i] = b[i-1]+a[i];
else b[i] = a[i];
ans = max(ans,b[i]);
}
printf("%d\n",ans);
}
return 0;
}
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2018/10/09/algorithm-experiment-2/