密码学中的数论
一群人找呀找,突然发现:最初等的数论很适合用于设计密码。
基础概念
整除
$b\mid a$ 表示 $b$ 整除 $a$,其中 $b$ 是 $a$ 的因数,$a$ 是 $b$ 的倍数。
整除符号 $\mid$ 可使用 LaTeX 代码
\mid。
性质:
- 若 $a\mid 1$,则 $a=\pm 1$
- 若 $a\mid b$ 且 $b\mid a$,则 $a=\pm b$
- 若 $b\ne 0$,则 $b\mid 0$,即 $0$ 是所有非零数的倍数
- 若 $a\mid b$ 且 $b\mid c$,则 $a\mid c$(传递性)
- 对任意整数 $m,n$,若 $b\mid g$ 且 $b \mid h$,则可得出 $b\mid (mg+nh)$
素数、算数基本定理
整数 $p>1$ 是素数,当且仅当它只有因子 $\pm 1$ 和 $\pm p$(通常忽略负数,即它的因子只有 $1$ 和它本身)。
算术基本定理:任意整数 $a>1$ 都可以唯一分解成下面形式:
其中,$p_1,p_2,\dots,p_t$ 均为素数,且 $p_1<p_2<\dots,p_t$ ,所有 $\alpha_i$ 均为正整数。
最大公因数、互素、欧几里得算法
$a$ 和 $b$ 的最大公因数是能同时整除 $a$ 和 $b$ 的最大整数,记为 $\gcd(a,b)$ 。
- $\gcd(b,0)=b$
在数论语境下可以省略 $\gcd$,直接将最大公因数记为 $(a,b)$ 的形式。
两个整数 $a$ 和 $b$ 是互素的,当且仅当它们只有一个正整数公因子 $1$ ,即 $\gcd(a,b)=1$ 。
求最大公因数常用欧几里得算法:
- 若 $a\bmod b=0$,则 $\gcd(a,b)=b$
- 当 $a\bmod b\ne 0$,则递归计算 $\gcd(a,b)=\gcd(b,a\bmod b)$
Python 代码:
def gcd(a, b):
if b == 0:
return a
return gcd(b, a%b)
随机数互素概率
两个随机数互素的概率约为 $0.6$ 。
推导如下。
令 $P=\Pr\left[\gcd(a,b)=1 \right]$ 。
任取两个随机数 $a$ 和 $b$,设 $\gcd(a,b)=d$ ,可以做如下等价变换。
在所有整数中随机选取一个数 $n$,满足 $d\mid n$ 的概率为 $1/d$ 。则:
$d$ 可取任意正整数,将所有情况的概率加起来应为 1,有:
而有以下恒等式结论可用:
所以:
模运算、同余
定义比 $n$ 小的非负数集合为 $\mathbb{Z}_n=\left\{0,1,\dots,(n-1) \right\}$,称为模 $n$ 的完全剩余系(简称完系)。它的每一个元素代表一个剩余类。
整数集 $\mathbb{Z}$ 的 LaTeX 代码为
\mathbb{Z}。
同余与整除:若 $n\mid (a-b)$,则 $a\equiv b\pmod{n}$
模运算性质:
- $\left[(a\bmod n)+(b\bmod n) \right]\bmod n=(a+b)\bmod n$
- $\left[(a\bmod n)\times (b\bmod n) \right]\bmod n=(a\times b)\bmod n$
同余式中的模的 LaTeX 代码为
\pmod{n},模运算的 LaTeX 代码为\bmod。
费马小定理
Fermat’s little theorem
若 $a$ 是一个整数,$p$ 是一个素数,那么:
若 $a$ 不是 $p$ 的倍数,即满足 $\gcd(a,p)=1$,那么:
欧拉函数
Euler’s totient function
欧拉函数 $\varphi(n)$ 是小于等于 $n$ 的正整数中,与 $n$ 互素的数的个数。
希腊字母 $\varphi$ 读作
phi,LaTeX 代码为\varphi。
- $\varphi(1) = 1$
- 若 $p$ 为素数,则 $\varphi(p)=p-1$
- 若 $p$ 为素数,则 $\varphi(p^\alpha)=p^\alpha-p^{\alpha-1}$
- 若 $\gcd(m,n)=1$,则 $\varphi(m\times n)=\varphi(m)\times\varphi(n)$
一般公式:
- 若 $n=p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}$,
- 则 $\varphi(n)=\prod_{i=1}^{r} p_{i}^{k_{i}-1}\left(p_{i}-1\right)$ 。
推导:
- 欧拉函数 $\varphi(n)$ 是小于等于 $n$ 的正整数中,与 $n$ 互素的数的个数。
- 若 $n=1$,小于等于它的正整数只有 $1$,且 $\gcd(1,1)=1$,所以 $\varphi(1)=1$。
- 若 $n$ 为素数,因为 $n$ 与小于它的任何正整数都是互素的,所以 $\varphi(n)=n-1$。
- 若 $n=p^k$,其中 $p$ 为素数,此时当一个数不是 $p$ 的倍数时,它与 $n$ 互素。$[1,n]$ 中共有 $n=p^k$ 个正整数,其中 $p$ 的倍数有 $p,2\cdot p,\dots,p^{k-1}\cdot p$,共 $p^{k-1}$ 个,所以 $\varphi(n)=p^k-p^{k-1}=p^{k-1}(p-1)$。
- 若 $\gcd(m,n)=1$,根据 CRT,$\mathbb{Z}_{m\times n}^{\ast}$ 和 $\mathbb{Z}_m^{\ast}\times \mathbb{Z}_n^{\ast}$ 构成一一映射,所以 $\varphi(m\times n)=\varphi(m)\times \varphi(n)$。
所以,对于 $n=p_{1}^{k_{1}} p_{2}^{k_{2}} \cdots p_{r}^{k_{r}}$,其中 $p_1,p_2,\dots p_r$ 为互不相同的素数,由以上推导可知:
实际上就是 $n$ 的简化剩余系(也称既约剩余系或缩系,reduced residue system,符号为 $\mathbb{Z}_n^{\ast}$)中的元素个数。
欧拉定理
Euler’s theorem
若正整数 $n,a$ 互素(即 $\gcd(n,a)=1$),那么:
其中,$\varphi(n)$ 为欧拉函数。
素性检验
常用 Miller-Rabin 算法。
两个基础理论:
- 费马小定理:若 $p$ 为素数,且 $\gcd(a,p)=1$,则 $a^{p-1}\equiv 1\pmod{p}$ 。
- 二次探测定理:若 $p$ 是一个素数,$0<x<p$,则方程 $x^2\equiv 1\pmod{p}$ 的解为 $x\equiv 1\pmod p$ 或 $x\equiv p-1\pmod{p}$ 。
二次探测定理的证明
若 $p$ 为素数,那么 $p$ 不可被拆分为几个素数的乘积,有 $p\mid (x+1)$ 或 $p\mid (x-1)$ 成立。所以 $x\equiv 1\pmod{p}$ 或 $x\equiv p-1\pmod{p}$ 。
若 $p$ 不是素数,则不一定成立(可能因数会被拆到两项中)。
Miller-Rabin 算法
要测试一个奇数 $n\ge 3$ 是否为素数,可将 $n-1$ 表示为:
其中,$s$ 和 $d$ 都是正整数,且 $d$ 是奇数。
在每次测试开始时,随机选一个整数 $a$ ,$1<a<n-1$。
若满足以下条件的一种,则判定 $n$ 有可能是素数:
其中,$r=0,~1,\dots,~s-1$。(注意:只要其中有一个 $r$ 使得第二个式子成立,则判定 $n$ 有可能是素数)
Q: 你说它有可能是素数,具体的概率是多大?
A: 通过一次测试,判定待测数为有可能是素数的概率是小于 $1/4$ 的,那么通过 $t$ 次测试($a$ 取不同值)都判定为有可能是素数的概率是小于 $(1/4)^t$ 的。因此,通过多次测试,则有很大把握说 $n$ 是素数($n$ 有不可忽略的概率为素数)。
原理
将 $n-1$ 分解为 $2^sd$,其中 $d$ 为奇数。
根据费马小定理,若 $n$ 为素数,则 $a^{n-1}\equiv a^{2^sd} \equiv 1\pmod{n}$ 成立。
根据二次探测定理,若 $n$ 为素数,则对于以下数列:
最后一个数要为 $1$,且每一个数都是前一个数的平方(对 $n$ 取模),因此下面两条必有一条是正确的:
- 数列的第一个数为 $1$,那么其后的所有数都为 $1$。
- 数列中($a^{2^s d}$之前)有一数为 $n-1$,那么其后的所有数都为 $1$。(因为 $-1$ 的平方是 $1$)
Q: 直接检测 $a^{2^s d}\bmod n=1$ 是否成立不香吗?干嘛还要这么麻烦?
A: 少年,我们要的是效率!你想想看是不是计算低次幂比高次幂更快。事实上,一般要计算高次幂,为了提高效率也是先计算低次幂。
伪代码
MR(n)
分解n-1 = 2^{s}d
随机选择整数a (1<a<n-1)
if a^{d} mod n = 1
return 有可能是素数
for j = 0 to s-1
if a^{2^{j}d} mod n = n-1
return 有可能是素数
return 是合数
例子:判断29是不是素数
对于一个素数 $n=29$,有 $n-1=28=2^2\cdot 7=2^s d$,得到 $s=2,~d=7$ 。
第一次测试,选择一个数 $a=10$ 。
计算 $10^7\bmod 29=17$,既不为 $1$ 也不为 $28$ 。
计算$(10^7)^2\bmod 29=28$,因此返回「有可能是素数」。
第二次测试,选择一个数 $a=2$ 。
计算 $2^7\bmod 29=12$,既不为 $1$ 也不为 $28$ 。
计算 $(2^7)^2\bmod 29=28$,因此返回「有可能是素数」。
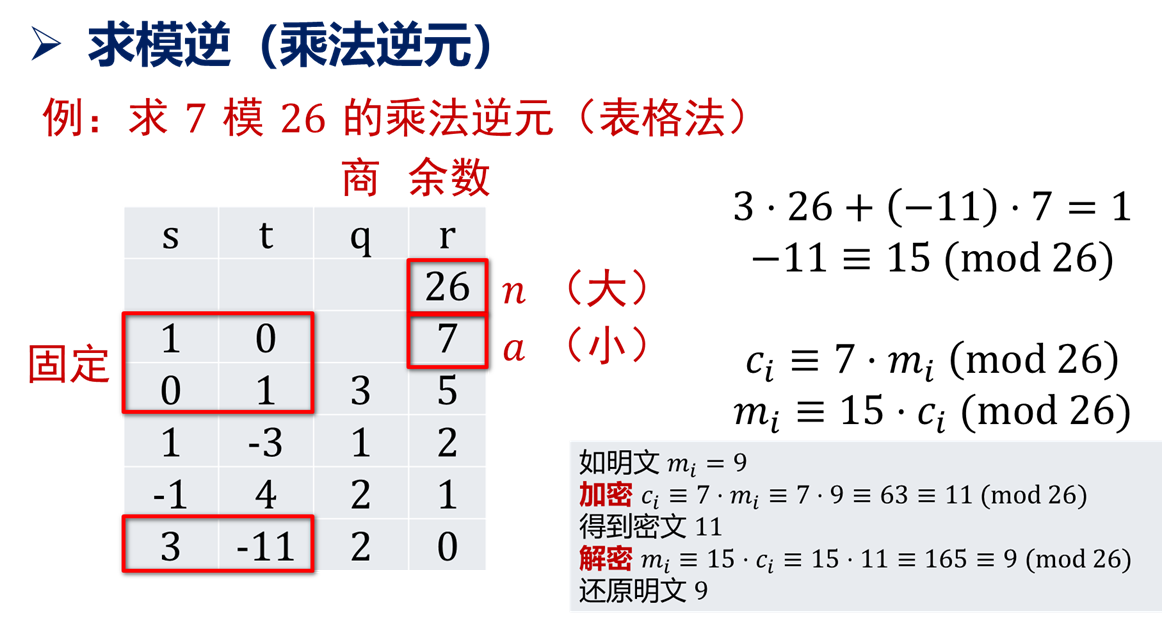
扩展欧几里得算法
Extended Euclidean algorithm
用于求有限域上的乘法逆元。
直接上实例,原理如下:

为了方便计算和书写,通常写为表格:
可以试试例题:
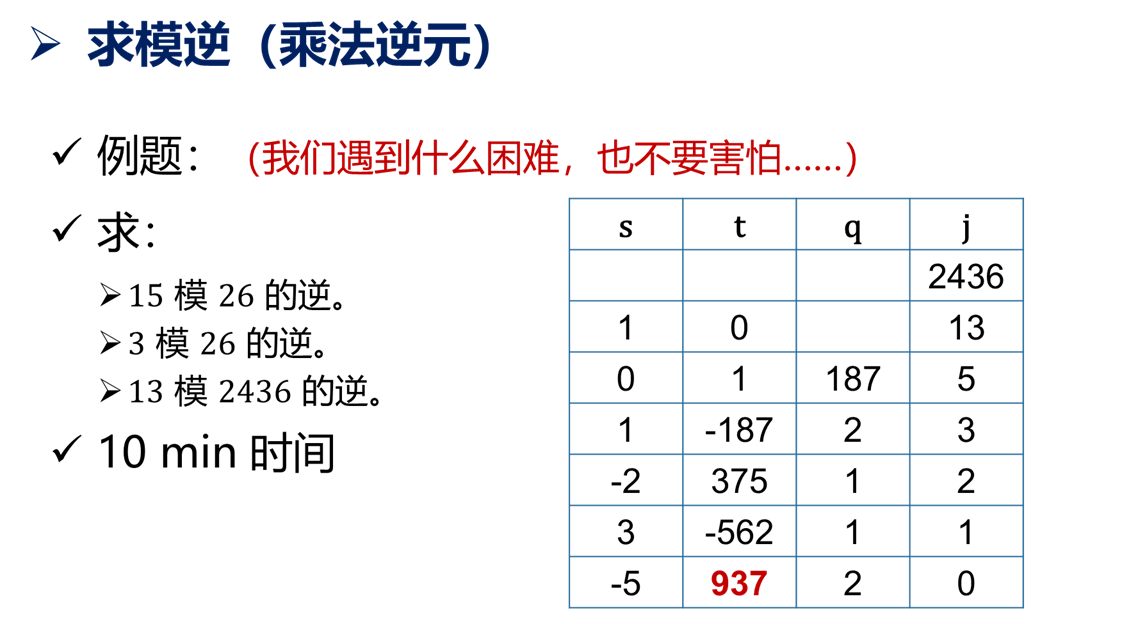
计算复杂度:$O(\log^3 n)$
Python 3.8+ 原生支持求模逆:
pow(9, -1, 29)
要求 $\operatorname{GF}(2^m)$ 上的乘法逆元式,稍微复杂点。不过其实只是把数换为多项式了。
题干会给出一个不可约的模式 $m(x)$ 。
注意,运算过程中所有系数都是在 $\operatorname{GF}(2)$ 上的,即只能取 0 或 1 。
中国剩余定理
Chinese Remainder Theorem, CRT
也叫孙子定理。
有一同余方程组:
有解的条件:(模数两两互素)若模数 $m_1,~m_2,\dots,~m_n$ 两两互素,则该同余方程组有解。
Q: 不满足两两互素怎么办?
A: 想办法让它们两两互素!
令 $M$ 为所有模数的乘积,即 $M=m_1\times m_2\times\cdots\times m_n$,设 $M_i=M/m_i$。
设 $M_i^{\prime}$ 为 $M_i$ 模 $m_i$ 的乘法逆元,即$M_i^{\prime}=(M_i^{-1}\bmod m_i)$。
在模 $M$ 的意义下,方程组只有一个解:
注意,最后解出来是在模 $M$ 的意义下!
CRT 可用于提升 RSA 解密速度(提升 4 倍左右),因为解密指数 $d$ 通常很大,要计算 $m=c^d\bmod n$,可以把模数 $n$ 拆为 $p\times q$,结合欧拉定理可以较快计算 $c^d\bmod p$ 和 $c^d\bmod p$,然后 CRT 回去就是 $m$ 了。
CRT 可用于带门限的秘密共享方案。
原根、离散对数问题
Primitive root modulo $n$
原根、生成元、本原根,都是一个意思。
若一个数的阶为 $\varphi(n)$,则称它为 $n$ 的本原根。
群内一个元素 $a$ 的阶是使得 $a^{m}=\mathrm{e}$ 成立的最小正整数 $m$,其中 $\mathrm{e}$ 为这个群的单位元。
若 $a$ 是 $n$ 的本原根,则模 $n$ 下 $a$ 的 $1$ 到 $(n-1)$ 各次幂恰能生成 $1$ 到 $(n-1)$ 的每个数,且每个数仅出现一次。
形象地说,假设 $a$ 是 $n$ 的一个本原根,那么:
是:
的一个排列。
因此,模 $n$ 下对任意整数 $b$ 和 $n$ 的本原根 $a$,有唯一的幂 $i$ ($0\le i\le p-1$)使得:
那么指数 $i$ 称为以 $a$ 为底(模数为 $n$)的离散对数,记为 $\operatorname{dlog}_{a,n}(b)$ 。
与实数上的对数 $\log$ 相似,显然有以下结论:
- $\operatorname{dlog}_{a,n}(1)=0$
- $\operatorname{dlog}_{a,n}(a)=1$
由欧拉定理,若 $\gcd(a,n)=1$,则 $a^{\varphi(n)}\equiv1\pmod{n}$ ,不难得出 $a$ 的阶一定为 $\varphi(n)$ 的因数。
所以只需要对 $\varphi(n)$ 的每个真因数 $d$ 验证 $a^d\equiv 1\pmod{n}$ 是否成立即可:
- 若有一个真因数 $d$ 使上述条件成立,则 $a$ 就不是原根
- 若都不成立,则 $a$ 是原根
若一个数有原根,则它的所有原根个数为 $\varphi\left(\varphi(n) \right)$ 。
求原根例题:

什么数有原根?只有形如 $2,~4,~p^l$ 或 $2p^l$ 的数才有原根,其中 $p$ 为任意奇素数,$l$ 是正整数。
$34$ 以内的数的原根列表:
| $n$ | $n$ 的原根 | 周期 $=\varphi(n)$ |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 2 |
| 5 | 2, 3 | 4 |
| 6 | 5 | 2 |
| 7 | 3, 5 | 6 |
| 9 | 2, 5 | 6 |
| 10 | 3, 7 | 4 |
| 11 | 2, 6, 7, 8 | 10 |
| 13 | 2, 6, 7, 11 | 12 |
| 14 | 3, 5 | 6 |
| 17 | 3, 5, 6, 7, 10, 11, 12, 14 | 16 |
| 18 | 5, 11 | 6 |
| 19 | 2, 3, 10, 13, 14, 15 | 18 |
| 22 | 7, 13, 17, 19 | 10 |
| 23 | 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 | 22 |
| 25 | 2, 3, 8, 12, 13, 17, 22, 23 | 20 |
| 26 | 7, 11, 15, 19 | 12 |
| 27 | 2, 5, 11, 14, 20, 23 | 18 |
| 29 | 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 | 28 |
| 31 | 3, 11, 12, 13, 17, 21, 22, 24 | 30 |
| 34 | 3, 5, 7, 11, 23, 27, 29, 31 | 16 |
离散对数表举例:要求以 $2$ 为底,模为 $19$ 的离散对数表。
先打出下表:
| $i$ | $2^i\bmod 19$ |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 13 |
| 6 | 7 |
| 7 | 14 |
| 8 | 9 |
| 9 | 18 |
| 10 | 17 |
| 11 | 15 |
| 12 | 11 |
| 13 | 3 |
| 14 | 6 |
| 15 | 12 |
| 16 | 5 |
| 17 | 10 |
| 18 | 1 |
交换两列,以 $a$ 升序排列,可以得到以 $2$ 为底,模为 $19$ 的离散对数表:
| $a$ | $\operatorname{dlog}_{2,19}(a)$ |
|---|---|
| 1 | 18 |
| 2 | 1 |
| 3 | 13 |
| 4 | 2 |
| 5 | 16 |
| 6 | 14 |
| 7 | 6 |
| 8 | 3 |
| 9 | 8 |
| 10 | 17 |
| 11 | 12 |
| 12 | 15 |
| 13 | 5 |
| 14 | 7 |
| 15 | 11 |
| 16 | 4 |
| 17 | 10 |
| 18 | 9 |
考虑方程:
给定 $g,~x$ 和 $p$,可直接计算出 $y$,换句话说,正向过程是容易计算的。
但是,给定 $y,~g$ 和 $p$,计算 $x$ 非常困难,这就是所谓的「离散对数」困难问题。
应用:
- Diffie-Hellman
- ElGamal
不可约多项式
Irreducible polynomial
多项式中的不可约多项式,相当于正整数中的素数。
系数在 $\operatorname{GF}(2)$ 上且零次项为 1 的不可约多项式有:
- $x+1$
- $x^{2}+x+1$
- $x^3+x^2+1$
- $x^3+x+1$
- ……
由于:
所以,它们两个都是可约多项式。
判断是否可约可以挨个尝试除以比他小的所有(不可约)多项式。
例如:要判断 $x^4+1$ 是否可约,首先除以 $(x+1)$,余式为 $0$,商式为 $(x^3+x^2+x+1)$,所以它为可约多项式。
群、环、域基本概念
群 $\{G,~\cdot\}$
Group
定义一个二元运算 $\cdot$ ,$G$ 中的每一个序偶 $(a,b)$ 通过运算生成 $G$ 中的元素 $(a\cdot b)$,满足下列公理:
- [A1] 封闭性:若 $a$ 和 $b$ 都属于 $G$,则 $a\cdot b$ 也属于 $G$
- [A2] 结合律:$a\cdot (b\cdot c)=(a\cdot b)\cdot c$
- [A3] 单位元:$G$ 中存在元素 $e$,对于 $G$ 中任意元素 $a$,都有 $a\cdot e=e\cdot a=a$ 成立
- [A4] 逆元:对于 $G$ 中任意元素 $a$,$G$ 中都存在一个元素 $a^{\prime}$,使得 $a\cdot a^{\prime}=a^{\prime}\cdot a=e$ 成立
如果一个群的元素是有限的,则该群称为有限群,群的阶等于群中元素的个数。
反之,如果一个群的元素是无限的,则该群称为无限群。
若一个群满足交换律,则称它为交换群,或阿贝尔群。
- [A5] 交换律:$a\cdot b =b\cdot a$
如果群中的每一个元素都是一个固定的元素 $a\in G$ 的幂 $a^k, ~k\in \mathbb{Z}$,则称 $G$ 为循环群,称 $a$ 为生成元。
环 $\{R,~+,~\times\}$
Ring
具有 $+$ 和 $\times$ 两个二元运算的集合,满足:
- [A1-A5] 关于加法是一个交换群,单位元是 $0$,$a$ 的逆是 $-a$
- [M1] 乘法封闭性:若 $a$ 和 $b$ 都属于 $R$,则 $a\times b$ 也属于 $R$
- [M2] 乘法结合律:$a\times(b\times c)=(a\times b)\times c$
- [M3] 乘法分配律:$a(b+c)=ab+ac$ 或者 $(a+b)c=ac+bc$
若一个环满足乘法交换律,则称它为交换环。
- [M4] 乘法交换律:$a\times b=b\times a$
若一个环是交换环,还具有乘法单位元,且无零因子,则其是一个整环。
- [M5] 乘法单位元:$R$ 中存在元素 $1$ 使得对于所有 $a$ 都有 $a1=1a=a$ 成立
- [M6] 无零因子:如果 $R$ 中有 $a,~b$ 且 $ab=0$,则 $a=0$ 或 $b=0$
域 $\{F,~+,~\times\}$
Field
具有 $+$ 和 $\times$ 两个二元运算的集合,满足:
- [A1-M6] $F$ 是一个整环
- [M7] 乘法逆元:对于 $F$ 中除 $0$ 外的任意元素 $a$,$F$ 中都存在一个元素 $a^{-1}$,使得 $aa^{-1}=a^{-1}a=1$
性质:在其上进行加减乘除不会脱离该集合。
- 除法:$a/b=ab^{-1}$
群、环、域的关系概览:
再度
(失踪人口回归)
小学的时候,老师总和我们说:好记性不如烂笔头。
实践是检验真理的唯一标准。
经过十多年的求学生涯的实践检验,我可以推断这句话没毛病。
因为对密码学中的基础知识有做一定记录,所以即使忘了,还可以翻翻博客和笔记温习。
不过对于数论,我就基本没留下什么痕迹,故可以说我也在试图通过本文弥补这方面遗憾吧。
本科时候学的很浅的《信息安全数学基础》让我一度有数论学得很好的自信。不过好像其他学校信安也没多学什么。
然而随着时间的推移,以前很熟悉的知识都忘了或不太熟练了。反映了写笔记的重要性。
对于素性检验中最常用的 Miller-Rabin 算法,之前把算法背过,但对原理比较模糊,于是花了好长时间重新学习,弄清原理。我原来觉得很一般的书(主要是觉得中文版带一股翻译腔,且缺失很多重要内容)《密码编码学与网络安全——原理与实践》竟发挥了重要作用。
将笔记写在博客上,有什么好处呢?我想了想,主要有三个:
- 只要能联网,就能查看之前的笔记;
- 方便他人学习,同时受到他人检验;
- 留下痕迹,积攒回忆。
感谢来自熟悉或是陌生的人的鼓励。






从2018年4月本站上线到现在(2020年12月16日),一共积攒了 12k+ 的浏览量:
(数据看起来还不错呀)
随手翻阅以前做的笔记,感觉以前对知识的理解确实要比现在要好。
这离不开反复搜寻资料和推导加深理解,更离不开老师的循循善诱。
真的觉得我现在的文字能力变弱了。(怀古伤今)
但是,要相信,会越来越好哒!要以乐观主义的心态面对生活,要相信明天一定比今天更好。
就让时间去检验一切吧!(很巧的是实践恰好与时间谐音)
I’m an old physicist. I’m not afraid of death. I’m afraid of time.
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2020/12/16/num-theory-crypto/
